KAlgebra/Console Tab/uk: Difference between revisions

From KDE UserBase Wiki
(Updating to match new version of source page)
(Created page with "Після виконання цієї команди у f міститимуться лише елементи у проміжку від -0,5 до +0,5. Перший арг...")
 
(42 intermediate revisions by 2 users not shown)
Line 2: Line 2:
== Знайомимося з консоллю ==
== Знайомимося з консоллю ==


The '''KAlgebra''' console tab is the first thing you see when you open the '''KAlgebra''' program. It is like a calculator, but way better. The small edit field at the very bottom of the screen is the input bar. It is used to input the the problem that you want to solve. The answer is shown in the display area in the middle of the screen. On the right, there is a medium sized window which is the variable window. This shows the current values of the variables, such as: pi, true, false, and even the current answer. The console can be used to make simple and complex calculations, and it's easier and quicker than bringing up a calculator function. In order to do calculations, you enter the equation you want to be solved into the input bar. After you press <keycap>Enter</keycap> it will show you the answer in the display area.
Вкладка консолі '''KAlgebra''' є типовою вкладкою, яку ви бачитимете одразу після запуску програми '''KAlgebra'''. Вона чимось подібна до калькулятора, але є набагато зручнішою. Невеличке поле для редагування у нижній частині вкладки призначено для введення команд. До цього поля слід вводити ваші питання до програми. Відповідь на них буде показано у середній частині вкладки. Праворуч на вкладці розташовано панель змінних. На ній буде показано поточні значення змінних, зокрема pi, true, false в поточне значення відповіді на питання. Консоллю можна скористатися для виконання простих і складних обчислень, вона є простішою та швидшою за звичайний калькулятор. Для виконання обчислень вам достатньо ввести відповідне рівняння до рядка введення. Після натискання клавіші <keycap>Enter</keycap> на панелі показу ви побачите результат обчислень.


=== Equals!! or Equals? that is the Question ===
=== Дорівнює або чи дорівнює? Ось у чому питання ===


One of the main things you must know about '''KAlgebra''' is the difference between ''equals!'' and ''equals?'' I know what you're thinking, “What's the difference?”. Well, "equals!" (:=) is used to set or define the value of the variable you have chosen. For example, <code>y:=3</code> defines y as equal to 3. ''Equals?'' (=) means you are inquiring as to whether or not a variable is equal to that value. You will receive either the answer true or the answer false in this case. For example, if you input <code>y:= 3</code>, then enter <code>y=2</code>, your answer you will get will be “'''false'''”. So, := is the operator that '''KAlgebra''' uses to ''define'', and = is the ''logical'' operator (that goes along with < > <= and >=).
Однією з основних речей, які вам слід знати про '''KAlgebra''', є відмінність між командою ''дорівнює!'' і питанням ''дорівнює?'' Звичайно ж, ви могли подумати: «А в чому ж відмінність?» Гаразд, «дорівнює!» (:=) використовується для встановлення значення або визначення змінної, якою ви хочете скористатися. Наприклад, <code>y:=3</code> визначає, що y дорівнює 3. ''Дорівнює?'' (=) означає, що ви просите програму перевірити, чи дорівнює змінна вказаному значенню. У відповідь на ваше питання буде повернуто відповідь «так» (true) або «ні» (false). Наприклад, якщо ви введете код <code>y:= 3</code>, а потім код <code>y=2</code>, відповіддю буде “'''false'''”. Отже, := — оператор, який у '''KAlgebra''' використовується для ''визначення'', а = — ''логічний'' оператор (оператор, подібний до < > <= та >=).


=== KAlgebra as a Kwicker Kalculator ===
=== KAlgebra — швидкий калькулятор ===


There are also basic calculator functions such as, addition (+), subtraction (-), multiplication (*), division (/), exponents (**) and(^), and order of operations () [Please Excuse My Dear Aunt Sally ;-)]. If you want to take the square root of a number, you type the number followed by ^0.5. For example, the square root of five: 25^0.5. When using a calculator program on the computer you must mouse around the different virtual key. '''KAlgebra's''' console allows you to just type in what you want to solve which is much faster and more direct.
Передбачено також типові функції калькулятора, зокрема додавання (+), віднімання (-), множення (*), ділення (/), піднесення до степеня (**) та (^), а також дужки для визначення порядку операцій. Якщо вам потрібно обчислити квадратний корінь з числа, допишіть до нього ^0.5. Наприклад, обчислити квадратний корінь з двадцяти п’яти можна так: 25^0.5. Під час користування графічними калькуляторами вам доведеться весь час наводити вказівник миші на віртуальні клавіші. У консолі ж '''KAlgebra''' вам достатньо просто вводити команди, що може бути набагато швидшими та безпосереднішим способом обміну даними з програмою.


=== Setting up User Functions with the Lambda Operator ===
=== Визначення функцій, вказаних користувачем, за допомогою лямбда-оператора ===


The lambda operator is difficult to wrap your head around at first glance. Basically, it is the way to define a new function in the KAlgebra console. The best way to discuss how to use it is by example. An example of what the area of a rectangle would look like would be:  
З першого погляду лямбда-оператори можуть здатися абсолютно незрозумілими. Насправді ж, це просто спосіб визначити нову функцію у консолі '''KAlgebra'''. Найкращим способом зрозуміти таке визначення є приклад. Таким прикладом може бути функція обчислення площі прямокутника:  


{{Input|1=<nowiki>AreaRect:=(b,h)->b*h </nowiki>}}
{{Input|1=<nowiki>AreaRect:=(b,h)->b*h </nowiki>}}


What I did here is define (:=) the function AreaRect. AreaRect is a function of two free variables b and h (base and height). The lambda operator (->) shows how they are mapped into the area of a rectangle. After you key this function in, the AreaRect function is built into '''KAlgebra'''. Go ahead, type in, <code>AreaRect(4,2)</code>, you will get the answer, 8.
Тут ми просто визначили (:=) функцію AreaRect. AreaRect є функцією двох довільних змінних, b і h (ширини і висоти). Лямбда-оператор (->) показує, як вони перетворюються у площу прямокутника. Після введення цієї функції AreaRect вважатиметься вбудованою функцією '''KAlgebra'''. Якщо ви, наприклад, введете <code>AreaRect(4,2)</code>, комп’ютер покаже вам відповідь, 8.


Below is a screen shot showing how this most basic of functions is defined, displayed in the variable list, utilized by the user, with results shown in the display.
Нижче наведено знімок вікна з визначенням цієї найпростішої функції, списком змінних, використаних користувачем та результатами, показаними програмою.


[[File:Kalgebra-lambda-example.png]]
[[File:Kalgebra-lambda-example_uk.png]]


=== Help! (or is it Help?) ===
=== Довідка! (або чи допоможе довідка?) ===


The dictionary is the best source for all of '''KAlgebra's''' available functions. You just click the dictionary tab, and you will get a list of all 64 functions. If you want to edit the value of a variable, you can double click on the current value in the variables list and enter anything you want. '''KAlgebra''' includes an auto complete feature which will suggest possible functions you may use for your calculations. It starts working when you begin typing in the input bar. Once you type in at least one letter, it will give you several options as to what you may want to enter. If one of those options is suitable, you click on it, and what you've been typing will be automatically completed.
Найкращим джерелом щодо властивостей доступних у '''KAlgebra''' функцій є вкладка '''Словник'''. На цій вкладці ви знайдете список всіх доступних 64 функцій. Якщо вам захочеться змінити значення змінної, просто наведіть вказівник миші на її пункт у списку змінних, двічі клацніть лівою кнопкою миші і введіть потрібне вам значення. У '''KAlgebra''' передбачено можливість автоматичного доповнення коду, за допомогою якої програма пропонуватиме можливі варіанти на основі відомих їй функцій. Ця можливість почне працювати, щойно ви введете якийсь код у поле для введення команд. Достатньо ввести принаймні одну літеру, і ви побачите декілька варіантів можливого продовження. Якщо один з цих варіантів є прийнятним, просто наведіть на нього вказівник миші і клацніть лівою кнопкою: ваш код буде автоматично дописано до визначеного варіанта.


=== The Ultimate Example of Math Geekery ===
=== Повний приклад заплутаних математичних обчислень ===


To show some of the '''KAlgebra''' console concepts, we would like to find the area under a sine curve. To do so, we are going to estimate the area as the area of a bunch of trapezoids that fit under the sine curve. For starters, we define a function (f) that provides our sine curve from 0 to 3.14 radians:
Для демонстрації декількох можливостей консолі '''KAlgebra''' давайте обчислимо площу під графіком синуса. Ми знайдемо площу наближено за допомогою методу трапецій, сума площ яких наближено дорівнює площі під кривою. Для початку визначимо функцію (f), яка даватиме значення синуса на проміжку аргументів від 0 до 3,14:


{{Input|1=<nowiki>f:=x->sin(x)</nowiki>}}
{{Input|1=<nowiki>f:=x->sin(x)</nowiki>}}


We didn't have to do this, we could just use sin(x) directly, but we can also replace sin(x) in the definition of f to find the area of other interesting shapes.
Визначати окрему функцію необов’язково, ми могли просто скористатися безпосередньо функцією sin(x), але у нашому прикладі sin(x) у визначенні f можна просто замінити і знайти площу під кривою іншої цікавої для нас функції.


Next we define a function that is able to calculate the area of a trapezoid:
Далі, ми визначимо функцію, за допомогою якої можна шукати площу трапеції:


{{Input|1=nowiki>A:=(b,h1,h2)->0.5*(h1+h2)*b</nowiki>}}
{{Input|1=<nowiki>A:=(b,h1,h2)->0.5*(h1+h2)*b</nowiki>}}


The above function is a function of three variables (base, height 1, and height 2) that '''KAlgebra''' is more than capable of handling.  
Визначена вище функція є функцією трьох змінних (довжини висоти трапеції (b) і довжин основ (h_1 і h_2)). Отже, '''KAlgebra''' може працювати з функціями декількох змінних.  


Next, we are going to evaluate the series of trapezoids beneath the sine curve in increments of 0.01 radians. To help us do this, we define a helper function x(k)=0.01*k or:
Далі, нам потрібна буде послідовність трапецій під синусоїдою з кроком у 0,01 радіан. Введемо допоміжну функцію x(k)=0,01*k або:


{{Input|1=<nowiki>x:=k->0.01*k</nowiki>}}
{{Input|1=<nowiki>x:=k->0.01*k</nowiki>}}


So that as k counts from 0 to 314, x changes from 0 to 3.14 radians. We sum the trapezoid areas up using sum function:  
Отже, k приймає значення від 0 до 314, x змінюється від 0 до 3,14 радіан. Суму площ трапецій знайдемо за допомогою функції sum:  


{{Input|1=<nowiki>sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)</nowiki>}}
{{Input|1=<nowiki>sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)</nowiki>}}


This shows off a lot of '''KAlgebra's''' capabilities and syntax. You can see the use of the built in function, sum. We show off the use of nested functions. Also, we see the use of the ''range'' syntax.
У цьому прикладі показано значну частину можливостей та синтаксичних конструкцій '''KAlgebra'''. Ми познайомилися з використанням вбудованої функції, sum, було показано використання вкладених функцій. Також у цьому прикладі показано синтаксичні конструкції для визначення ''діапазонів''.


[[File:Kalgebra-sinearea-example.png]]
[[File:Kalgebra-sinearea-example_uk.png]]


Our answer is very close to two, which happens to be the exact solution.  
Отримане нами значення є доволі близьким до точної відповіді — 2.  


=== Recursion ===
=== Рекурсія ===


See, Recursion.
Див. рекурсія.


OK, seriously, to understand recursion, you must first understand recursion. The '''KAlgebra''' console provides the user with a virtual laboratory for experimenting with and using recursion. Probably the most used example of recursion is the factorial. Below we define our own factorial function using '''KAlgebra's''' capabilities for defining functions, performing logic inside of functions, and having a function call itself, which is the definition of recursion:
Гаразд, якщо перейти до серйозної розмови, для розуміння рекурсії вам слід розуміти рекурсію. Консоль '''KAlgebra''' може бути віртуальною лабораторією для експериментів з використанням рекурсії. Ймовірно, найпоширенішим прикладом рекурсивних обчислень є обчислення факторіала. Нижче ми визначимо власну функцію факторіала за допомогою можливостей '''KAlgebra''' з визначення функцій, визначення логічних конструкцій функцій та самого виклику функції, яку визначено рекурсивно:


{{Input|1=<nowiki>fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}</nowiki>}}
{{Input|1=<nowiki>fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}</nowiki>}}


So, breaking this down, we're defining our own function (fact) which just so happens to call fact. This takes advantage of the recursive definition of the factorial function.
Отже, якщо простіше, ми визначаємо нашу власну функцію (fact), яка викликає функцію fact. Таким чином, ми користуємося рекурсивною природою визначення факторіала.


fact(n) = n! = n*(n-1)*(n-2)*...*2*1
fact(n) = n! = n*(n-1)*(n-2)*...*2*1


Noting that (n-1)! = (n-1)*(n-2)*...*2*1,
Зауважуючи, що (n-1)! = (n-1)*(n-2)*...*2*1, маємо: n! = n*(n-1)! або fact(n) = n*fact(n-1)
we have: n! = n*(n-1)!  
or fact(n) = n*fact(n-1)


To stop the chain of calculations, we define that 1! = 1. We accomplish this bit of logic using the piecewise{ expression ? value, expression ? value, ..., ? default value} construct.
Останнім кроком наших обчислень має бути визначення 1! = 1. Для такого типу логічних конструкцій ми використовуємо такий код: piecewise{ вираз ? значення, вираз ? значення, ..., ? типове значення}.


[[File:Kalgebra-recursion-example.png]]
[[File:Kalgebra-recursion-example_uk.png]]


=== Fun with Lists ===
=== Розважаємося зі списками ===


Beginning with version 0.11, '''KAlgebra''' comes with advanced (and by advanced, I mean time saving) list operations. '''KAlgebra''' had previously come with the means of entering a list of variables or values. For example, one could enter a list of numbers as follows:
Починаючи з версії 0.11, у '''KAlgebra''' передбачено досконаліші способи (досконалішими ми вважаємо такі способи, за допомогою яких можна зекономити час на введення команд) виконання дій зі списками. У попередніх версіях '''KAlgebra''' список змінних або значень можна було ввести як звичайний список. Наприклад, можна було ввести список чисел так:


{{Input|1=<nowiki>x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}</nowiki>}}
{{Input|1=<nowiki>x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}</nowiki>}}


Now, with the '''map''' function, '''KAlgebra''' provides the user with the means of applying a function to each element of the list. As a simple example, one might wish to evaluate the sine of each element of the list. One might also be tempted to enter '''sin(x)'''. One would be disappointed.
Тепер же, за допомогою функції '''map''' користувач '''KAlgebra''' може застосовувати певну функцію до кожного з елементів у списку. Задля простого прикладу знайдемо синус кожного з елементів у списку. Можна було б припустити, що слід ввести команду '''sin(x)''', але це не так.


To apply a function to each element of the list we use the map function as follows:  
Щоб застосувати функцію до кожного з елементів у списку, слід скористатися функцією map ось так:  


{{Input|1=<nowiki>s := map( u->sin(u), x)</nowiki>}}
{{Input|1=<nowiki>s := map( u->sin(u), x)</nowiki>}}


The first argument of the map function sets up the function that will be applied to all elements of the list given in the second argument of the map function. So now, '''s''' is a list holding the sine of every element of x.
За допомогою першого з аргументів функції map визначається функція, яку буде застосовано до всіх елементів списку, вказаного за допомогою другого аргументу функції map. Отже, тепер у '''s''' зберігається список синусів кожного з елементів x.


If we want to pare down a list we can use the filter function to select the list elements we want to keep:
Якщо нам потрібно відсіяти зі списку зайві елементи, ми можемо скористатися функцією filter для вибору тих елементів, які слід залишити у списку:


{{Input|1=<nowiki>f := filter( u-> and(u>=-0.5,u<=0.5), s)</nowiki>}}
{{Input|1=<nowiki>f := filter( u-> and(u>=-0.5,u<=0.5), s)</nowiki>}}


After this, f will contain only elements of s that are between -0.5 and +0.5. The first argument of the filter function defines a logical operation used to select the values of the list that we want.
Після виконання цієї команди у f міститимуться лише елементи у проміжку від -0,5 до +0,5. Перший аргумент функції filter визначає логічну операцію, яку буде використано для вибору значень з потрібного нам списку.


Below is a screenshot of the various list operations discussed:
Нижче наведено знімок вікна програми з виконаними діями над списками, які ми обговорювали вище.


[[File:Kalgebra-listopsoxy-example.png]]  
[[File:Kalgebra-listopsoxy-example_uk.png]]  




=== Parting Words ===
=== Декілька завершальних слів ===


We have scratched the surface of the wonders presented by the '''KAlgebra''' user console. There is a lot of stuff that can be done, so roll up your sleeves, and do some math!
Ми лише торкнулися всіх тих чудових можливостей, доступ до яких можна отримати за допомогою консолі '''KAlgebra'''. За її допомогою можна досягти багатьох корисних результатів, отже вам варто засукати рукави і перейти до справи!


--[[User:Trlanzi|trLanzi]] 01:10, 1 December 2011 (UTC)
--[[User:Trlanzi|trLanzi]] 01:10, 1 December 2011 (UTC)


[[Category:Education]]
[[Category:Освіта/uk]]
[[Category:Tutorials]]
[[Category:Підручники/uk]]

Latest revision as of 17:11, 20 October 2012

Other languages:

Знайомимося з консоллю

Вкладка консолі KAlgebra є типовою вкладкою, яку ви бачитимете одразу після запуску програми KAlgebra. Вона чимось подібна до калькулятора, але є набагато зручнішою. Невеличке поле для редагування у нижній частині вкладки призначено для введення команд. До цього поля слід вводити ваші питання до програми. Відповідь на них буде показано у середній частині вкладки. Праворуч на вкладці розташовано панель змінних. На ній буде показано поточні значення змінних, зокрема pi, true, false в поточне значення відповіді на питання. Консоллю можна скористатися для виконання простих і складних обчислень, вона є простішою та швидшою за звичайний калькулятор. Для виконання обчислень вам достатньо ввести відповідне рівняння до рядка введення. Після натискання клавіші Enter на панелі показу ви побачите результат обчислень.

Дорівнює або чи дорівнює? Ось у чому питання

Однією з основних речей, які вам слід знати про KAlgebra, є відмінність між командою дорівнює! і питанням дорівнює? Звичайно ж, ви могли подумати: «А в чому ж відмінність?» Гаразд, «дорівнює!» (:=) використовується для встановлення значення або визначення змінної, якою ви хочете скористатися. Наприклад, y:=3 визначає, що y дорівнює 3. Дорівнює? (=) означає, що ви просите програму перевірити, чи дорівнює змінна вказаному значенню. У відповідь на ваше питання буде повернуто відповідь «так» (true) або «ні» (false). Наприклад, якщо ви введете код y:= 3, а потім код y=2, відповіддю буде “false”. Отже, := — оператор, який у KAlgebra використовується для визначення, а = — логічний оператор (оператор, подібний до < > <= та >=).

KAlgebra — швидкий калькулятор

Передбачено також типові функції калькулятора, зокрема додавання (+), віднімання (-), множення (*), ділення (/), піднесення до степеня (**) та (^), а також дужки для визначення порядку операцій. Якщо вам потрібно обчислити квадратний корінь з числа, допишіть до нього ^0.5. Наприклад, обчислити квадратний корінь з двадцяти п’яти можна так: 25^0.5. Під час користування графічними калькуляторами вам доведеться весь час наводити вказівник миші на віртуальні клавіші. У консолі ж KAlgebra вам достатньо просто вводити команди, що може бути набагато швидшими та безпосереднішим способом обміну даними з програмою.

Визначення функцій, вказаних користувачем, за допомогою лямбда-оператора

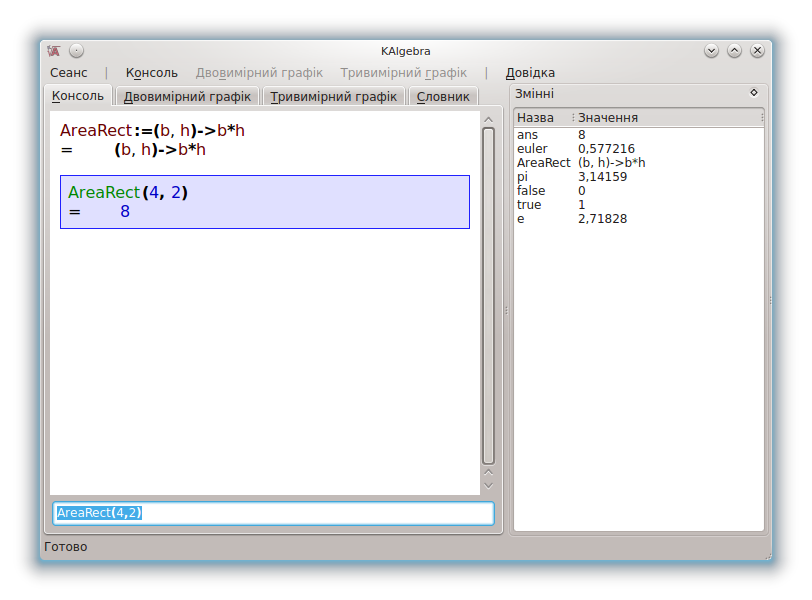
З першого погляду лямбда-оператори можуть здатися абсолютно незрозумілими. Насправді ж, це просто спосіб визначити нову функцію у консолі KAlgebra. Найкращим способом зрозуміти таке визначення є приклад. Таким прикладом може бути функція обчислення площі прямокутника: 

AreaRect:=(b,h)->b*h

Тут ми просто визначили (:=) функцію AreaRect. AreaRect є функцією двох довільних змінних, b і h (ширини і висоти). Лямбда-оператор (->) показує, як вони перетворюються у площу прямокутника. Після введення цієї функції AreaRect вважатиметься вбудованою функцією KAlgebra. Якщо ви, наприклад, введете AreaRect(4,2), комп’ютер покаже вам відповідь, 8.

Нижче наведено знімок вікна з визначенням цієї найпростішої функції, списком змінних, використаних користувачем та результатами, показаними програмою.

Довідка! (або чи допоможе довідка?)

Найкращим джерелом щодо властивостей доступних у KAlgebra функцій є вкладка Словник. На цій вкладці ви знайдете список всіх доступних 64 функцій. Якщо вам захочеться змінити значення змінної, просто наведіть вказівник миші на її пункт у списку змінних, двічі клацніть лівою кнопкою миші і введіть потрібне вам значення. У KAlgebra передбачено можливість автоматичного доповнення коду, за допомогою якої програма пропонуватиме можливі варіанти на основі відомих їй функцій. Ця можливість почне працювати, щойно ви введете якийсь код у поле для введення команд. Достатньо ввести принаймні одну літеру, і ви побачите декілька варіантів можливого продовження. Якщо один з цих варіантів є прийнятним, просто наведіть на нього вказівник миші і клацніть лівою кнопкою: ваш код буде автоматично дописано до визначеного варіанта.

Повний приклад заплутаних математичних обчислень

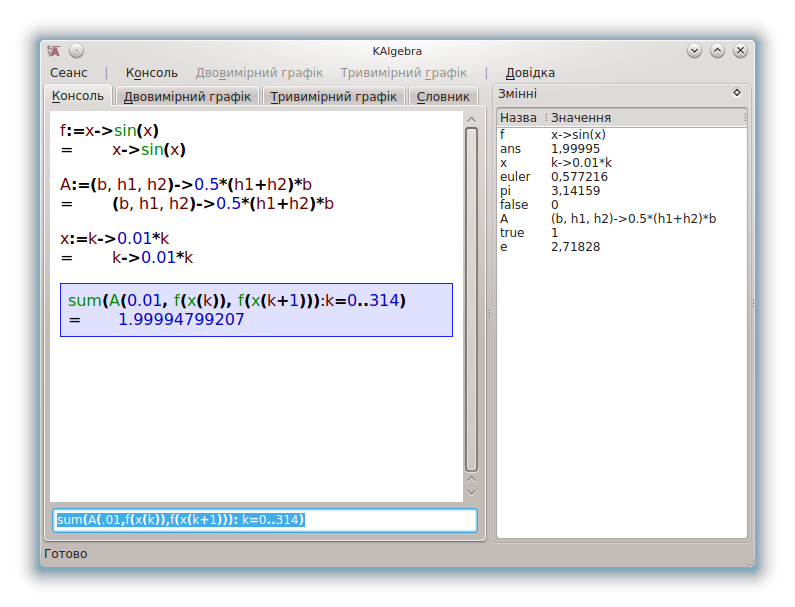
Для демонстрації декількох можливостей консолі KAlgebra давайте обчислимо площу під графіком синуса. Ми знайдемо площу наближено за допомогою методу трапецій, сума площ яких наближено дорівнює площі під кривою. Для початку визначимо функцію (f), яка даватиме значення синуса на проміжку аргументів від 0 до 3,14: 

f:=x->sin(x)

Визначати окрему функцію необов’язково, ми могли просто скористатися безпосередньо функцією sin(x), але у нашому прикладі sin(x) у визначенні f можна просто замінити і знайти площу під кривою іншої цікавої для нас функції.

Далі, ми визначимо функцію, за допомогою якої можна шукати площу трапеції: 

A:=(b,h1,h2)->0.5*(h1+h2)*b

Визначена вище функція є функцією трьох змінних (довжини висоти трапеції (b) і довжин основ (h_1 і h_2)). Отже, KAlgebra може працювати з функціями декількох змінних.

Далі, нам потрібна буде послідовність трапецій під синусоїдою з кроком у 0,01 радіан. Введемо допоміжну функцію x(k)=0,01*k або: 

x:=k->0.01*k

Отже, k приймає значення від 0 до 314, x змінюється від 0 до 3,14 радіан. Суму площ трапецій знайдемо за допомогою функції sum: 

sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)

У цьому прикладі показано значну частину можливостей та синтаксичних конструкцій KAlgebra. Ми познайомилися з використанням вбудованої функції, sum, було показано використання вкладених функцій. Також у цьому прикладі показано синтаксичні конструкції для визначення діапазонів.

Отримане нами значення є доволі близьким до точної відповіді — 2.

Рекурсія

Див. рекурсія.

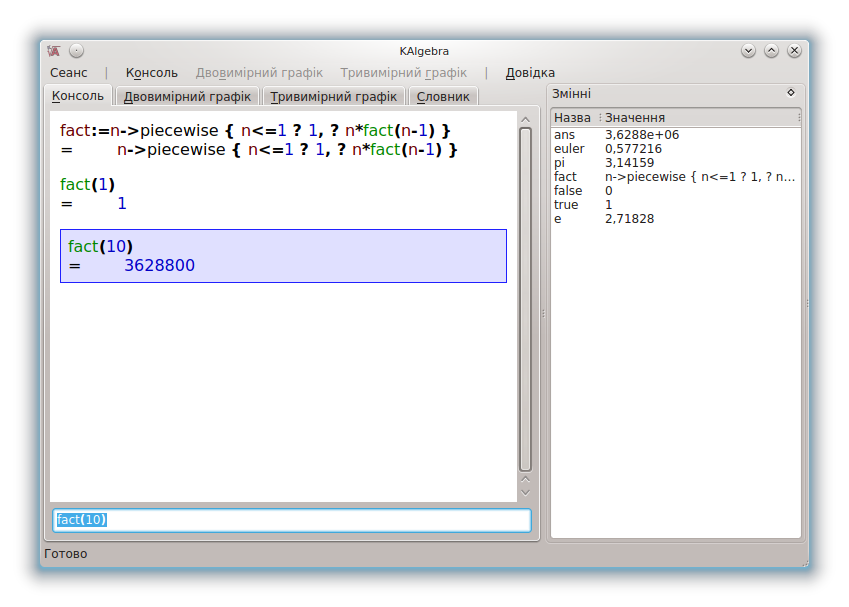
Гаразд, якщо перейти до серйозної розмови, для розуміння рекурсії вам слід розуміти рекурсію. Консоль KAlgebra може бути віртуальною лабораторією для експериментів з використанням рекурсії. Ймовірно, найпоширенішим прикладом рекурсивних обчислень є обчислення факторіала. Нижче ми визначимо власну функцію факторіала за допомогою можливостей KAlgebra з визначення функцій, визначення логічних конструкцій функцій та самого виклику функції, яку визначено рекурсивно: 

fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}

Отже, якщо простіше, ми визначаємо нашу власну функцію (fact), яка викликає функцію fact. Таким чином, ми користуємося рекурсивною природою визначення факторіала.

fact(n) = n! = n*(n-1)*(n-2)*...*2*1

Зауважуючи, що (n-1)! = (n-1)*(n-2)*...*2*1, маємо: n! = n*(n-1)! або fact(n) = n*fact(n-1)

Останнім кроком наших обчислень має бути визначення 1! = 1. Для такого типу логічних конструкцій ми використовуємо такий код: piecewise{ вираз ? значення, вираз ? значення, ..., ? типове значення}.

Розважаємося зі списками

Починаючи з версії 0.11, у KAlgebra передбачено досконаліші способи (досконалішими ми вважаємо такі способи, за допомогою яких можна зекономити час на введення команд) виконання дій зі списками. У попередніх версіях KAlgebra список змінних або значень можна було ввести як звичайний список. Наприклад, можна було ввести список чисел так: 

x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}

Тепер же, за допомогою функції map користувач KAlgebra може застосовувати певну функцію до кожного з елементів у списку. Задля простого прикладу знайдемо синус кожного з елементів у списку. Можна було б припустити, що слід ввести команду sin(x), але це не так.

Щоб застосувати функцію до кожного з елементів у списку, слід скористатися функцією map ось так: 

s := map( u->sin(u), x)

За допомогою першого з аргументів функції map визначається функція, яку буде застосовано до всіх елементів списку, вказаного за допомогою другого аргументу функції map. Отже, тепер у s зберігається список синусів кожного з елементів x.

Якщо нам потрібно відсіяти зі списку зайві елементи, ми можемо скористатися функцією filter для вибору тих елементів, які слід залишити у списку: 

f := filter( u-> and(u>=-0.5,u<=0.5), s)

Після виконання цієї команди у f міститимуться лише елементи у проміжку від -0,5 до +0,5. Перший аргумент функції filter визначає логічну операцію, яку буде використано для вибору значень з потрібного нам списку.

Нижче наведено знімок вікна програми з виконаними діями над списками, які ми обговорювали вище.


Декілька завершальних слів

Ми лише торкнулися всіх тих чудових можливостей, доступ до яких можна отримати за допомогою консолі KAlgebra. За її допомогою можна досягти багатьох корисних результатів, отже вам варто засукати рукави і перейти до справи!

--trLanzi 01:10, 1 December 2011 (UTC)

Retrieved from "https://userbase.kde.org/index.php?title=KAlgebra/Console_Tab/uk&oldid=271311"