KAlgebra/Console Tab
Getting to Know the Console
The KAlgebra console tab is the first thing you see when you open the KAlgebra program. It is like a calculator, but way better. The small edit field at the very bottom of the screen is the input bar. It is used to input the the problem that you want to solve. The answer is shown in the display area in the middle of the screen. On the right, there is a medium sized window which is the variable window. This shows the current values of the variables, such as: pi, true, false, and even the current answer. The console can be used to make simple and complex calculations, and it's easier and quicker than bringing up a calculator function. In order to do calculations, you enter the equation you want to be solved into the input bar. After you press Enter it will show you the answer in the display area.
Equals!! or Equals? that is the Question
One of the main things you must know about KAlgebra is the difference between equals! and equals? I know what you're thinking, “What's the difference?”. Well, "equals!" (:=) is used to set or define the value of the variable you have chosen. For example, y:=3 defines y as equal to 3. Equals? (=) means you are inquiring as to whether or not a variable is equal to that value. You will receive either the answer true or the answer false in this case. For example, if you input y:= 3, then enter y=2, your answer you will get will be “false”. So, := is the operator that KAlgebra uses to define, and = is the logical operator (that goes along with < > <= and >=).
KAlgebra as a Kwicker Kalculator
There are also basic calculator functions such as, addition (+), subtraction (-), multiplication (*), division (/), exponents (**) and(^), and order of operations () [Please Excuse My Dear Aunt Sally ;-)]. If you want to take the square root of a number, you type the number followed by ^0.5. For example, the square root of twentyfive: 25^0.5. When using a calculator program on the computer you must mouse around the different virtual key. KAlgebra's console allows you to just type in what you want to solve which is much faster and more direct.
Setting up User Functions with the Lambda Operator
The lambda operator is difficult to wrap your head around at first glance. Basically, it is the way to define a new function in the KAlgebra console. The best way to discuss how to use it is by example. An example of what the area of a rectangle would look like would be:
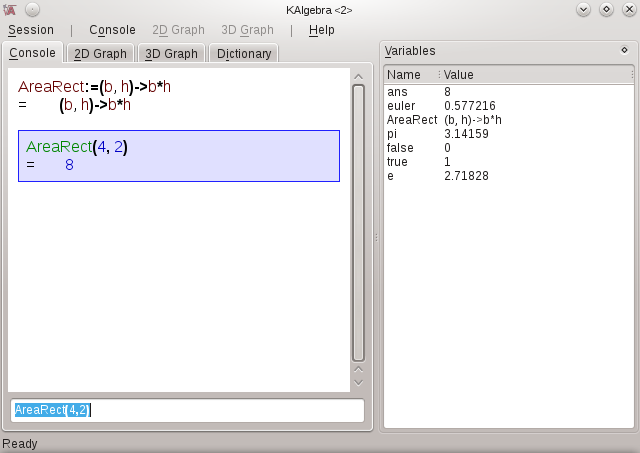
AreaRect:=(b,h)->b*h
What I did here is define (:=) the function AreaRect. AreaRect is a function of two free variables b and h (base and height). The lambda operator (->) shows how they are mapped into the area of a rectangle. After you key this function in, the AreaRect function is built into KAlgebra. Go ahead, type in, AreaRect(4,2), you will get the answer, 8.
Below is a screen shot showing how this most basic of functions is defined, displayed in the variable list, utilized by the user, with results shown in the display.
Help! (or is it Help?)
The dictionary is the best source for all of KAlgebra's available functions. You just click the dictionary tab, and you will get a list of all 64 functions. If you want to edit the value of a variable, you can double click on the current value in the variables list and enter anything you want. KAlgebra includes an auto complete feature which will suggest possible functions you may use for your calculations. It starts working when you begin typing in the input bar. Once you type in at least one letter, it will give you several options as to what you may want to enter. If one of those options is suitable, you click on it, and what you've been typing will be automatically completed.
The Ultimate Example of Math Geekery
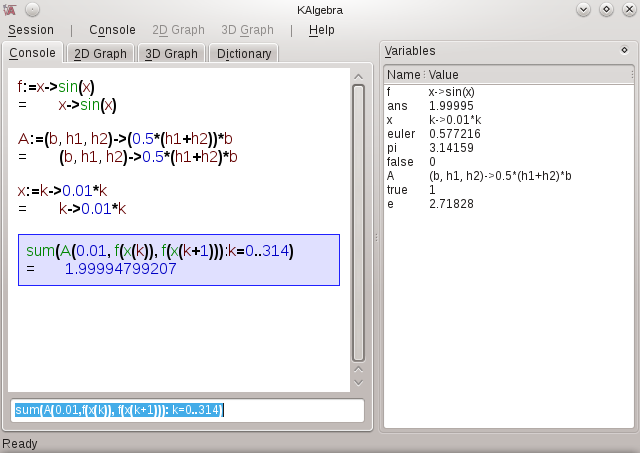
To show some of the KAlgebra console concepts, we would like to find the area under a sine curve. To do so, we are going to estimate the area as the area of a bunch of trapezoids that fit under the sine curve. For starters, we define a function (f) that provides our sine curve from 0 to 3.14 radians:
f:=x->sin(x)
We didn't have to do this, we could just use sin(x) directly, but we can also replace sin(x) in the definition of f to find the area of other interesting shapes.
Next we define a function that is able to calculate the area of a trapezoid:
A:=(b,h1,h2)->0.5*(h1+h2)*b
The above function is a function of three variables (base, height 1, and height 2) that KAlgebra is more than capable of handling.
Next, we are going to evaluate the series of trapezoids beneath the sine curve in increments of 0.01 radians. To help us do this, we define a helper function x(k)=0.01*k or:
x:=k->0.01*k
So that as k counts from 0 to 314, x changes from 0 to 3.14 radians. We sum the trapezoid areas up using sum function:
sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)
This shows off a lot of KAlgebra's capabilities and syntax. You can see the use of the built in function, sum. We show off the use of nested functions. Also, we see the use of the range syntax.
Our answer is very close to two, which happens to be the exact solution.
Recursion
See, Recursion.
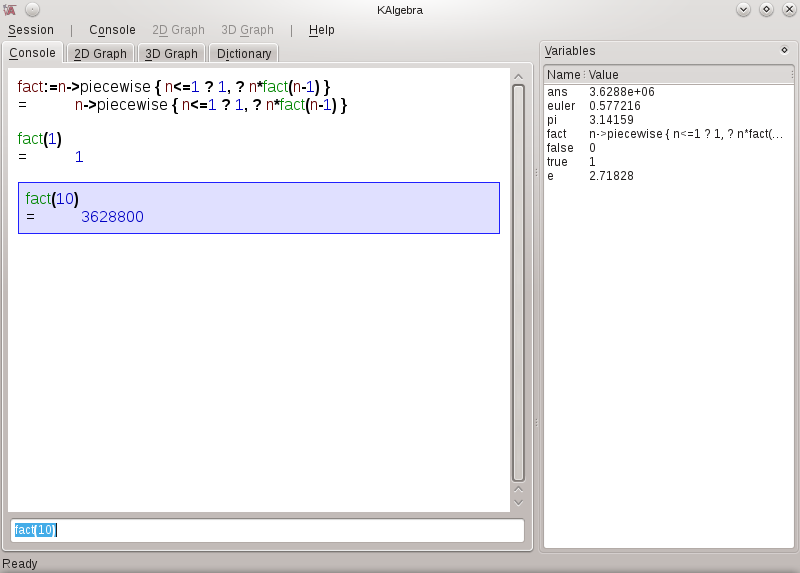
OK, seriously, to understand recursion, you must first understand recursion. The KAlgebra console provides the user with a virtual laboratory for experimenting with and using recursion. Probably the most used example of recursion is the factorial. Below we define our own factorial function using KAlgebra's capabilities for defining functions, performing logic inside of functions, and having a function call itself, which is the definition of recursion:
fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}
So, breaking this down, we're defining our own function (fact) which just so happens to call fact. This takes advantage of the recursive definition of the factorial function.
fact(n) = n! = n*(n-1)*(n-2)*...*2*1
Noting that (n-1)! = (n-1)*(n-2)*...*2*1, we have: n! = n*(n-1)! or fact(n) = n*fact(n-1)
To stop the chain of calculations, we define that 1! = 1. We accomplish this bit of logic using the piecewise{ expression ? value, expression ? value, ..., ? default value} construct.
Fun with Lists
Beginning with version 0.11, KAlgebra comes with advanced (and by advanced, I mean time saving) list operations. KAlgebra had previously come with the means of entering a list of variables or values. For example, one could enter a list of numbers as follows:
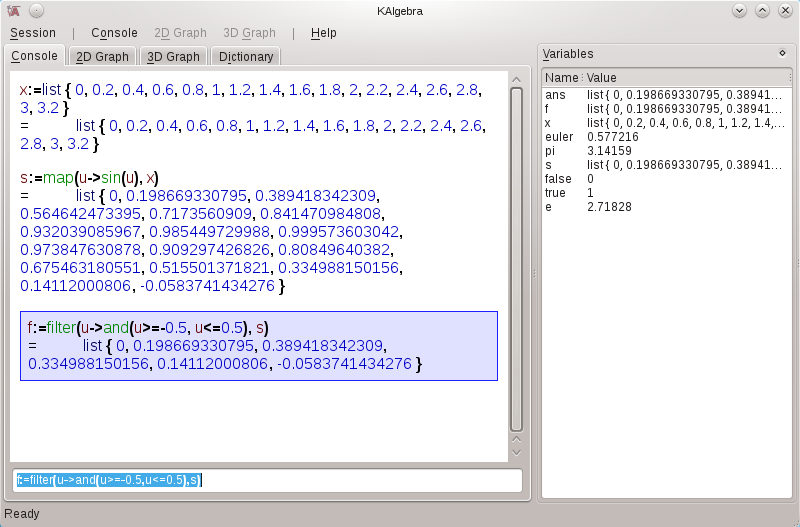
x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}
Now, with the map function, KAlgebra provides the user with the means of applying a function to each element of the list. As a simple example, one might wish to evaluate the sine of each element of the list. One might also be tempted to enter sin(x). One would be disappointed.
To apply a function to each element of the list we use the map function as follows:
s := map( u->sin(u), x)
The first argument of the map function sets up the function that will be applied to all elements of the list given in the second argument of the map function. So now, s is a list holding the sine of every element of x.
If we want to pare down a list we can use the filter function to select the list elements we want to keep:
f := filter( u-> and(u>=-0.5,u<=0.5), s)
After this, f will contain only elements of s that are between -0.5 and +0.5. The first argument of the filter function defines a logical operation used to select the values of the list that we want.
Below is a screenshot of the various list operations discussed:
Parting Words
We have scratched the surface of the wonders presented by the KAlgebra user console. There is a lot of stuff that can be done, so roll up your sleeves, and do some math!
--trLanzi 01:10, 1 December 2011 (UTC)