KAlgebra/Probabilities/uk: Difference between revisions
No edit summary |
No edit summary |
||
| (41 intermediate revisions by 2 users not shown) | |||
| Line 28: | Line 28: | ||
{{Input| | {{Input| | ||
2 | 2 2,778% | ||
3 | 3 5,556% | ||
4 | 4 8,333% | ||
5 | 5 11,111% | ||
6 | 6 13,889% | ||
7 | 7 16,667% | ||
8 | 8 13,889% | ||
9 | 9 11,111% | ||
10 8 | 10 8,333% | ||
11 | 11 5,556% | ||
12 2 | 12 2,778% | ||
}} | }} | ||
Чому ж, на відміну від випадку з однією кісткою, маємо різні значення ймовірностей для кожного з чисел? Відповідь дуже проста. Розглянемо результат «4» і всі комбінації з двох натуральних чисел, які у сумі дають 4: | |||
1+3 = 4 | 1+3 = 4 | ||
| Line 48: | Line 48: | ||
Таким чином, нам слід додати ймовірності кожної з цих комбінацій, щоб отримати загальну ймовірність випадання суми 4. Ось результат: | |||
P(1,3) + P(3,1) + P(2,2) = 1/6 * 1/6 + 1/6 * 1/6 + 1/6 * 1/6 = 0,08333 = 8,333% | |||
Отже, якщо у нас буде 5 кісток, нам доведеться додавати ймовірності для всіх варіантів чисел на 5 кістках, які у сумі дають потрібне нам число. Спосіб отримання ймовірностей сум для більшої кількості кісток є аналогічним. | |||
== | == Задача зі знаходження ймовірності == | ||
Розгляньмо задачу зі знаходження ймовірності випадання з п’яти кісток трьох з шістками. | |||
Знайти цю ймовірність можна таким чином: ймовірність випадання шістки на одній кістці * ймовірність випадання шістки на ще одній кістці * ймовірність випадання шістки на ще одній кістці * ймовірність випадання не шістки на одній кістці * ймовірність випадання не шістки на ще одній кістці | |||
Потрібна нам комбінація може бути такою: '''6 6 6 2 3''', або такою: '''5 6 6 6 1'''. Отже нам слід врахувати те, що нас задовольнятиме будь-який порядок випадання кісток, аби лише серед них було рівно три шістки. Тому слід ввести до розрахунків біноміальні коефіцієнти. | |||
Обчислити біноміальний коефіцієнт з '''N''' по '''M''' у '''KAlgebra''' можна таким чином: | |||
{{Input|1=factorial(N) / (factorial(M) * factorial(N-M))}} | {{Input|1=factorial(N) / (factorial(M) * factorial(N-M))}} | ||
Це комбінаторне число, яке визначається такою формулою: | |||
{{Input|1=comb:=(N,M)->factorial(N) / (factorial(M) * factorial(N-M))}} | {{Input|1=comb:=(N,M)->factorial(N) / (factorial(M) * factorial(N-M))}} | ||
Отже, біноміальний коефіцієнт для 3 чисел у 5 позиціях буде таким: | |||
{{Input|1=comb(5,3)}} | {{Input|1=comb(5,3)}} | ||
| Line 73: | Line 73: | ||
Отже наша функція набуде такого остаточного вигляду: | |||
{{Input|1=(comb(5, 3)*(1/6)*(1/6)*(1/6)*(5/6)*(5/6))}} | {{Input|1=(comb(5, 3)*(1/6)*(1/6)*(1/6)*(5/6)*(5/6))}} | ||
{{Output|1== 0.0321502}} | {{Output|1== 0.0321502}} | ||
Тепер ми можемо визначити просту функцію для отримання результату: | |||
{{Input|1=binomial:=(b, p, k)->(comb(b, k)*p^k)*(1-p)^(b-k)}} | {{Input|1=binomial:=(b, p, k)->(comb(b, k)*p^k)*(1-p)^(b-k)}} | ||
Отже тепер маємо: | |||
{{Input|1=binomial(5, 1/6,3)}} | {{Input|1=binomial(5, 1/6,3)}} | ||
{{Output|1== 0.0321502}} | {{Output|1== 0.0321502}} | ||
Це ймовірність отримати з п’яти елементарних подій (випадання певного числа на кістці) 3 сприятливих, якщо ймовірність сприятливого результату у елементарній події дорівнює 1/6, а ймовірність несприятливого — 5/6. | |||
Ви можете зауважити, що сума ймовірностей дорівнює 1: | |||
{{Input|1=sum(binomial(5,1/6,t):t=0..5)}} | {{Input|1=sum(binomial(5,1/6,t):t=0..5)}} | ||
| Line 95: | Line 95: | ||
У розподілі ймовірностей за значеннями величини ймовірностей спочатку зростають до максимального значення, а потім спадають. Форма розподілу нагадує форму дзвону. Такий розподіл ймовірностей називається [https://uk.wikipedia.org/wiki/Біноміальний_розподіл біноміальним розподілом]. | |||
Отже, тепер зрозуміло, що розподіл між можливими сумами на кістках не є рівномірним, тому вибір комбінацій з більшою ймовірністю випадання може вести до виграшу у грі з вгадування суми. | |||
Єдиним варіантом, коли всі результати є рівноймовірними, є варіант з однією кісткою, оскільки ймовірність випадання будь-якого числа у цьому випадку дорівнює 1/6. Ще одним прикладом такого рівномірного розподілу ймовірностей є підкидання монетки, коли ймовірність випадання будь-якої з її сторін дорівнює 1/2. | |||
Простим способом досягнення виграшу є збільшення ймовірності випадання потрібної грані. Наприклад, казино може додати невеличку вагу навпроти грані з шісткою, щоб ймовірності змінилися, скажімо так: | |||
{{Input| | {{Input| | ||
| Line 112: | Line 112: | ||
}} | }} | ||
Тепер, якщо ми викинемо 5 кісток, а нам потрібно буде три шістки, загальна ймовірність зміниться так: | |||
{{Input|1=binomial(5,0.25,3)}} | {{Input|1=binomial(5,0.25,3)}} | ||
| Line 118: | Line 118: | ||
[[Image:Kalgebra- | [[Image:Kalgebra-dice_uk.png|thumb|300px|right|Знімок вікна '''KAlgebra''' під час виконання обчислень ймовірностей]] | ||
=== | === Реалістичний приклад === | ||
Нехай маємо казино, яке грає проти гравця. | |||
Припустімо, що маємо також 5 кісток і початкову ставку у 1$. Тепер створимо правила гри таким чином: | |||
немає шісток або одна шістка: гравець програє 1$ | |||
дві або 3 шістки: гравець виграє 1$ | |||
чотири шістки: гравець виграє 175$ | |||
п’ять шісток: гравець виграє 375$ | |||
{|class=" | {|class="wikitable" style="border: 1px solid grey;" | ||
! | ! Кількість шісток | ||
! | ! Виграш або програш | ||
|- | |- | ||
| 0 | | 0 | ||
| Line 156: | Line 156: | ||
|} | |} | ||
Виконаємо розрахунок ймовірностей: | |||
Виграш гравця: | |||
Гравець виграє лише якщо випаде від двох до п’яти шісток. Отже, якщо рахувати ймовірність виграшу за допомогою '''KAlgebra''', матимемо: | |||
{{Input| | {{Input| | ||
| Line 170: | Line 170: | ||
Виграш казино: | |||
Казино виграє, якщо шістка не випаде або випаде один раз. Якщо рахувати виграш казино за допомогою '''KAlgebra''', матимемо: | |||
{{Input| | {{Input| | ||
| Line 181: | Line 181: | ||
}} | }} | ||
Тепер визначимо, чи є шанси на виграш збалансованими. | |||
Створимо функцію win(x), яка обчислюватиме відповідність між сумами ставок і ймовірностями виграшу: | |||
{{Input|1= | {{Input|1= | ||
| Line 188: | Line 188: | ||
}} | }} | ||
Давайте перевіримо наші обчислення за допомогою '''KAlgebra''': | |||
{{Input| | {{Input| | ||
| Line 197: | Line 197: | ||
}} | }} | ||
Результатом мав бути 0, але через похибки у внутрішньому представленні чисел у ком’ютері ми отримали лише близьке до нуля число. | |||
Як бачимо, у цьому випадку маємо гру з нульовою сумою: ні гравець, ні казино нічого не виграють, якщо гра продовжуватиметься нескінченно довго. | |||
[[Category:Освіта/uk]] | [[Category:Освіта/uk]] | ||
Latest revision as of 16:39, 8 October 2022
На цій сторінці наведено декілька прикладів використання KAlgebra для розв’язування задач теорії ймовірностей.
Вступ
Нехай ми ведемо гру 5 гральними кістками.

Теорія, яка лежить в основі гри
Спочатку проаналізуємо ситуацію з киданням однієї кістки:
Ймовірність отримати під час викидання будь-яке з чисел на кістці дорівнює 1/6 або 16,667%, оскільки ми маємо рівно 6 можливих результатів викидання і кожен з них є рівноймовірним з іншими.
Нижче наведено таблицю, де праворуч від числа на кістці записано ймовірність його випадання.
1 16,667%
2 16,667%
3 16,667%
4 16,667%
5 16,667%
6 16,667%
Якщо ми кидатимемо 2 кістки, розподіл ймовірностей, звичайно ж, зміниться:
2 2,778%
3 5,556%
4 8,333%
5 11,111%
6 13,889%
7 16,667%
8 13,889%
9 11,111%
10 8,333%
11 5,556%
12 2,778%
Чому ж, на відміну від випадку з однією кісткою, маємо різні значення ймовірностей для кожного з чисел? Відповідь дуже проста. Розглянемо результат «4» і всі комбінації з двох натуральних чисел, які у сумі дають 4:
1+3 = 4 3+1 = 4 2+2 = 4
Таким чином, нам слід додати ймовірності кожної з цих комбінацій, щоб отримати загальну ймовірність випадання суми 4. Ось результат:
P(1,3) + P(3,1) + P(2,2) = 1/6 * 1/6 + 1/6 * 1/6 + 1/6 * 1/6 = 0,08333 = 8,333%
Отже, якщо у нас буде 5 кісток, нам доведеться додавати ймовірності для всіх варіантів чисел на 5 кістках, які у сумі дають потрібне нам число. Спосіб отримання ймовірностей сум для більшої кількості кісток є аналогічним.
Задача зі знаходження ймовірності
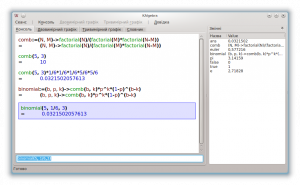
Розгляньмо задачу зі знаходження ймовірності випадання з п’яти кісток трьох з шістками.
Знайти цю ймовірність можна таким чином: ймовірність випадання шістки на одній кістці * ймовірність випадання шістки на ще одній кістці * ймовірність випадання шістки на ще одній кістці * ймовірність випадання не шістки на одній кістці * ймовірність випадання не шістки на ще одній кістці
Потрібна нам комбінація може бути такою: 6 6 6 2 3, або такою: 5 6 6 6 1. Отже нам слід врахувати те, що нас задовольнятиме будь-який порядок випадання кісток, аби лише серед них було рівно три шістки. Тому слід ввести до розрахунків біноміальні коефіцієнти. Обчислити біноміальний коефіцієнт з N по M у KAlgebra можна таким чином:
factorial(N) / (factorial(M) * factorial(N-M))
Це комбінаторне число, яке визначається такою формулою:
comb:=(N,M)->factorial(N) / (factorial(M) * factorial(N-M))
Отже, біноміальний коефіцієнт для 3 чисел у 5 позиціях буде таким:
comb(5,3)
= 10
Отже наша функція набуде такого остаточного вигляду:
(comb(5, 3)*(1/6)*(1/6)*(1/6)*(5/6)*(5/6))
= 0.0321502
Тепер ми можемо визначити просту функцію для отримання результату:
binomial:=(b, p, k)->(comb(b, k)*p^k)*(1-p)^(b-k)
Отже тепер маємо:
binomial(5, 1/6,3)
= 0.0321502
Це ймовірність отримати з п’яти елементарних подій (випадання певного числа на кістці) 3 сприятливих, якщо ймовірність сприятливого результату у елементарній події дорівнює 1/6, а ймовірність несприятливого — 5/6.
Ви можете зауважити, що сума ймовірностей дорівнює 1:
sum(binomial(5,1/6,t):t=0..5)
= 1
У розподілі ймовірностей за значеннями величини ймовірностей спочатку зростають до максимального значення, а потім спадають. Форма розподілу нагадує форму дзвону. Такий розподіл ймовірностей називається біноміальним розподілом.
Отже, тепер зрозуміло, що розподіл між можливими сумами на кістках не є рівномірним, тому вибір комбінацій з більшою ймовірністю випадання може вести до виграшу у грі з вгадування суми.
Єдиним варіантом, коли всі результати є рівноймовірними, є варіант з однією кісткою, оскільки ймовірність випадання будь-якого числа у цьому випадку дорівнює 1/6. Ще одним прикладом такого рівномірного розподілу ймовірностей є підкидання монетки, коли ймовірність випадання будь-якої з її сторін дорівнює 1/2.
Простим способом досягнення виграшу є збільшення ймовірності випадання потрібної грані. Наприклад, казино може додати невеличку вагу навпроти грані з шісткою, щоб ймовірності змінилися, скажімо так:
0.15 1
0.15 2
0.15 3
0.15 4
0.15 5
0.25 6
Тепер, якщо ми викинемо 5 кісток, а нам потрібно буде три шістки, загальна ймовірність зміниться так:
binomial(5,0.25,3)
= 0.087890625
Реалістичний приклад
Нехай маємо казино, яке грає проти гравця. Припустімо, що маємо також 5 кісток і початкову ставку у 1$. Тепер створимо правила гри таким чином:
немає шісток або одна шістка: гравець програє 1$
дві або 3 шістки: гравець виграє 1$
чотири шістки: гравець виграє 175$
п’ять шісток: гравець виграє 375$
| Кількість шісток | Виграш або програш |
|---|---|
| 0 | -1$ |
| 1 | -1$ |
| 2 | 1$ |
| 3 | 1$ |
| 4 | 175$ |
| 5 | 375$ |
Виконаємо розрахунок ймовірностей:
Виграш гравця:
Гравець виграє лише якщо випаде від двох до п’яти шісток. Отже, якщо рахувати ймовірність виграшу за допомогою KAlgebra, матимемо:
binomial(5,1/6,2)+binomial(5,1/6,3)+binomial(5,1/6,4)+binomial(5,1/6,5)
= 0.196244855967
Виграш казино:
Казино виграє, якщо шістка не випаде або випаде один раз. Якщо рахувати виграш казино за допомогою KAlgebra, матимемо:
binomial(5,1/6,0)+binomial(5,1/6,1)
= 0.803755144033
Тепер визначимо, чи є шанси на виграш збалансованими. Створимо функцію win(x), яка обчислюватиме відповідність між сумами ставок і ймовірностями виграшу:
win:=x->piecewise { x=0 ? -1, x=1 ? -1, x=2 ? 1, x=3 ? 1, x=4 ? 175, x=5 ? 375, ? 0 }
Давайте перевіримо наші обчислення за допомогою KAlgebra:
sum(win(x)*binomial(5,1/6,x): x=0..5)
= -2.01227923213e-16
Результатом мав бути 0, але через похибки у внутрішньому представленні чисел у ком’ютері ми отримали лише близьке до нуля число.
Як бачимо, у цьому випадку маємо гру з нульовою сумою: ні гравець, ні казино нічого не виграють, якщо гра продовжуватиметься нескінченно довго.
