KAlgebra: Difference between revisions
Pipesmoker (talk | contribs) |
Pipesmoker (talk | contribs) |
||
| Line 11: | Line 11: | ||
== The Console Tab == | == The Console Tab == | ||
When you first open KAlgebra a blank window shows up, this is the main work area for calculus. | When you first open '''KAlgebra''' a blank window shows up, this is the main work area for calculus. | ||
Let's get started with a little example of how KAlgebra works, just type: | Let's get started with a little example of how '''KAlgebra''' works, just type: | ||
{{Input|1=2+2}} | |||
Then type Return and KAlgebra will show you the result. So far it's easy. | Then type <keycap>Return</keycap> and '''KAlgebra''' will show you the result. So far it's easy. | ||
However, KAlgebra is much more powerful than that, it started as a simple calculator, but now it's almost a CAS. | However, '''KAlgebra''' is much more powerful than that, it started as a simple calculator, but now it's almost a CAS. | ||
You can define variables this way: | You can define variables this way: | ||
{{Input|1=k:=3 }} | |||
And use them normally: | And use them normally: | ||
{{Input|1=k*4}} | |||
And that will give you the result: 12 | And that will give you the result: 12 | ||
You can also define functions: | You can also define functions: | ||
{{Input|1=f:=x->x^2}} | |||
And then use them: | And then use them: | ||
{{Input|1=f(3)}} | |||
Which should return 9. | Which should return 9. | ||
You can define a function with as many variables as you want: | You can define a function with as many variables as you want: | ||
{{Input|1=g:=(x,y)->x*y}} | |||
The possibilities of defining functions are endless if you combine this with the piecewise. Let's define the factor function: | The possibilities of defining functions are endless if you combine this with the piecewise. Let's define the factor function: | ||
{{Input|1=fact:=n->piecewise { n=0 ? 1, n=1 ? 1, ? n*fact(n-1) } }} | |||
Yes! KAlgebra supports recursive functions. Give some values to n, to test it. | Yes! '''KAlgebra''' supports recursive functions. Give some values to n, to test it. | ||
{{Input|fact(5) | |||
fact(3)}} | |||
KAlgebra has recently started support for symbolic operations, to check it out, just type: | '''KAlgebra''' has recently started support for symbolic operations, to check it out, just type: | ||
{{Input|1=x+x+x+x}} | |||
or | or | ||
{{Input|1=x*x}} | |||
It doesn't work on some complex structures, though. Only basic support so far. | It doesn't work on some complex structures, though. Only basic support so far. | ||
Moreover, KAlgebra has support for differentiation. | Moreover, '''KAlgebra''' has support for differentiation. | ||
An example of the syntax: | An example of the syntax: | ||
{{Input|1=diff(x^2:x)}} | |||
If you have used KAlgebra, you will have noticed the syntax completion support, which is very helpful. | If you have used '''KAlgebra''', you will have noticed the syntax completion support, which is very helpful. | ||
Another resource that can be useful to learn more about KAlgebra comes with KAlgebra: The Dictionary tab | Another resource that can be useful to learn more about '''KAlgebra''' comes with '''KAlgebra''': The '''Dictionary''' tab. It contains examples of every function supported by '''KAlgebra'''. Maybe the best way to learn how to do things with '''KAlgebra'''. | ||
It contains examples of every function supported by KAlgebra. Maybe the best way to learn how to do things with KAlgebra. | |||
==Documentation== | ==Documentation== | ||
Revision as of 18:01, 4 July 2010
Home » Applications » Education » KAlgebra

|
KAlgebra is a calculator with symbolic and analysis features that lets you plot 2D and 3D functions as well as to easily calculate mathematical expressions.
It is part of the KDE Education Project. |
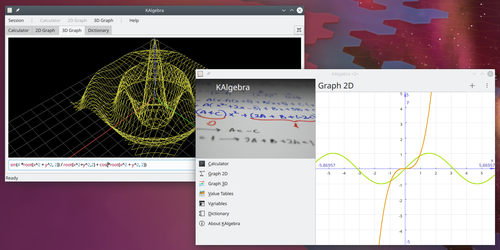
The Console Tab
When you first open KAlgebra a blank window shows up, this is the main work area for calculus.
Let's get started with a little example of how KAlgebra works, just type:
2+2
Then type Return and KAlgebra will show you the result. So far it's easy.
However, KAlgebra is much more powerful than that, it started as a simple calculator, but now it's almost a CAS. You can define variables this way:
k:=3
And use them normally:
k*4
And that will give you the result: 12 You can also define functions:
f:=x->x^2
And then use them:
f(3)
Which should return 9. You can define a function with as many variables as you want:
g:=(x,y)->x*y
The possibilities of defining functions are endless if you combine this with the piecewise. Let's define the factor function:
fact:=n->piecewise { n=0 ? 1, n=1 ? 1, ? n*fact(n-1) }
Yes! KAlgebra supports recursive functions. Give some values to n, to test it.
fact(5)
fact(3)
KAlgebra has recently started support for symbolic operations, to check it out, just type:
x+x+x+x
or
x*x
It doesn't work on some complex structures, though. Only basic support so far.
Moreover, KAlgebra has support for differentiation. An example of the syntax:
diff(x^2:x)
If you have used KAlgebra, you will have noticed the syntax completion support, which is very helpful.
Another resource that can be useful to learn more about KAlgebra comes with KAlgebra: The Dictionary tab. It contains examples of every function supported by KAlgebra. Maybe the best way to learn how to do things with KAlgebra.
