KAlgebra/Sandsynligheder
Denne side viser nogle anvendelser af KAlgebra på sandsynlighedsproblemer.
Introduktion
Lad os sige, at vi har 5 terninger og vi ønsker at spille hasard med dem.

Teorien bag spillet
Først må vi analysere en terning:
Sandsynligheden for at terningen viser et givet antal øjne er 1/6 eller 16,667% da hvert af de 6 mulige udfald er lige sandsynlige.
Sandsynligheden for at få hvert antal øjne er vist til højre
1 16.667%
2 16.667%
3 16.667%
4 16.667%
5 16.667%
6 16.667%
Når vi bruger to terninger, så ser de anderledes ud:
2 2.778%
3 5.556%
4 8.333%
5 11.111%
6 13.889%
7 16.667%
8 13.889%
9 11.111%
10 8.333%
11 5.556%
12 2.778%
Hvorfor er sandsynlighederne for hvert antal øjne så forskellige, spørger du måske. Svaret er enkelt. Lad os tage "4" som eksemple og finde alle kombinationer af to terninger med sum 4:
1+3 = 4 3+1 = 4 2+2 = 4
Vi skal altså lægge sandsynlighederne for disse begivenheder sammen for at få den samlede sandsynlighed for at få 4. Lad os teste dette:
Prob(1,3) + Prob(3,1) + Prob(2,2) = 1/6 * 1/6 + 1/6 * 1/6 + 1/6 * 1/6 = 0.08333 = 8,333%
Hvis vi har 5 terninger, så skal vi på tilsvarende måde finde antallet af måder at få hvert resultat på. Vi bruger så samme måde til at finde sandsynligheden for hver sum hvis der er et andet antal terninger.
Sandsynlighedsproblemet
Nu vil vi undersøge, hvad sandsynligheden for at få "6" 3 gange når vi kaster med 5 terninger.
Vi skal finde sandsynligheden for den første terning gange sandsynligheden for den anden gange sandsynligheden for den tredje gange sandsynligheden for den terning gange sandsynligheden for den femte \
Terningerne kan for eksempel viser 6 6 6 2 3, men de kan også være 5 6 6 6 1, så vi må bruge en binomialkoefficient til at tælle disse tilfælde. For at få binomialkoefficienten for at få M ud af N bruger vi følgende formel i KAlgebra:
factorial(N) / (factorial(M) * factorial(N-M))
Det kan vi definere således:
comb:=(N,M)->factorial(N) / (factorial(M) * factorial(N-M))
Binomialkoefficienten for at få 3 ud af 5 mulige er:
comb(5,3)
= 10
så vores endelige funktion bliver:
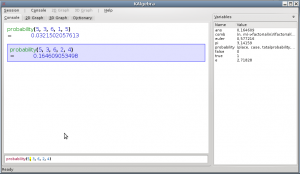
(comb(5, 3)*(1/6)*(1/6)*(1/6)*(5/6)*(5/6))
= 0.0321502
Vi kan nu definere en enkel funktion til at beregne resultatet:
binomial:=(b, p, k)->(comb(b, k)*p^k)*(1-p)^(b-k)
Så nu:
binomial(5, 1/6,3)
= 0.0321502
Dette er sandsynligheden for at få 3 seksere med 5 terninger når sandsynligheden for en terning er 1/6 og sandsynligheden for, at en terning ikke bliver en sekser dermed er 5/6
Vi kan bemærke at summen af sandsynlighederne er 1:
sum(binomial(5,1/6,t):t=0..5)
= 1
Vi kan se, at sandsynligheden vokser indtil den når en maksimumsværdi og derefter aftager igen. Vi ser en fordeling af sandsynlighederne blandt de mulige udfald. Denne slags fordeling kaldes en binomialfordeling.
Vi forstår nu, at spiller ikke er balanceret, at der er nogle udfald der er bedre end andre, så den der vælger den bedste har størst sandsynlighed for at vinde.
Den eneste måde at opnå et fair spil er ved kun at bruge en terning, hvor hvert udfald har sandsynligheden 1/6. En anden type spil med ligefordelte chancer er kast med en mønt, hvor begge de to sider har sandsynligheden 1/2.
A simple way where a player can win is to improve the probability on a face so it will be unbalanced, for istance the bank in a game can put a small load on the face with '6' so the probabilities change and the dice now became:
0.15 1
0.15 2
0.15 3
0.15 4
0.15 5
0.25 6
So now if we roll the 5 dices with this probability and we want 3 '6' to win the total probability is:
binomial(5,0.25,3)
= 0.087890625
Real World Example
There are two person, the bank and the player. Let's say they have 5 dices and the entrance fee for player is 1$. We can create a game like this:
0 to 1 times dice with '6': player loses 1$ with the fee
2 to 3 times dice with '6': player win 1$ with the fee
4 times dice with '6': player win 175$ with the fee
5 times dice with '6': player win 375$ with the fee
| k times '6' | win or loose |
|---|---|
| 0 | -1$ |
| 1 | -1$ |
| 2 | 1$ |
| 3 | 1$ |
| 4 | 175$ |
| 5 | 375$ |
Let's calculate the probability:
Probability for player:
The player can win only with 2-3 times 6, 4 times 6 or 5 times 6, so if we want to process the probability with KAlgebra it will be:
binomial(5,1/6,2)+binomial(5,1/6,3)+binomial(5,1/6,4)+binomial(5,1/6,5)
= 0.196244855967
Probability for bank:
The bank can win only with 0-1 times 6, so if we want to process the probability with KAlgebra it will be:
binomial(5,1/6,0)+binomial(5,1/6,1)
= 0.803755144033
We now want to see if player and bank are balanced, We create a function win(x), that create a correspondence between values and prizes:
win:=x->piecewise { x=0 ? -1, x=1 ? -1, x=2 ? 1, x=3 ? 1, x=4 ? 175, x=5 ? 375, ? 0 }
Let's verify the expression with KAlgebra:
sum(win(x)*binomial(5,1/6,x): x=0..5)
= -2.01227923213e-16
The result should be 0, but because of the internal representation of numbers in the computer the result is not exact.
As we can see the problem is equilibrated and player and bank will not win or lose anything for an infinite number of games.
