KmPlot/Using Sliders/uk: Difference between revisions
Appearance
Created page with "==Траєкторія руху снаряда==" |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
Тепер ви можете пересувати повзунок і спостерігати за тим, як значення параметра впливає на розташування кривої. | Тепер ви можете пересувати повзунок і спостерігати за тим, як значення параметра впливає на розташування кривої. | ||
<gallery perrow="3" caption=" | <gallery perrow="3" caption="Знімки вікон"> | ||
Image:Kmplot_function_with_param_uk.png|Введення даних | Image:Kmplot_function_with_param_uk.png|Введення даних | ||
Image:Kmplot_view_show_sliders_uk.png|Позначаємо пункт показу повзунків | Image:Kmplot_view_show_sliders_uk.png|Позначаємо пункт показу повзунків | ||
| Line 21: | Line 21: | ||
==Траєкторія руху снаряда== | ==Траєкторія руху снаряда== | ||
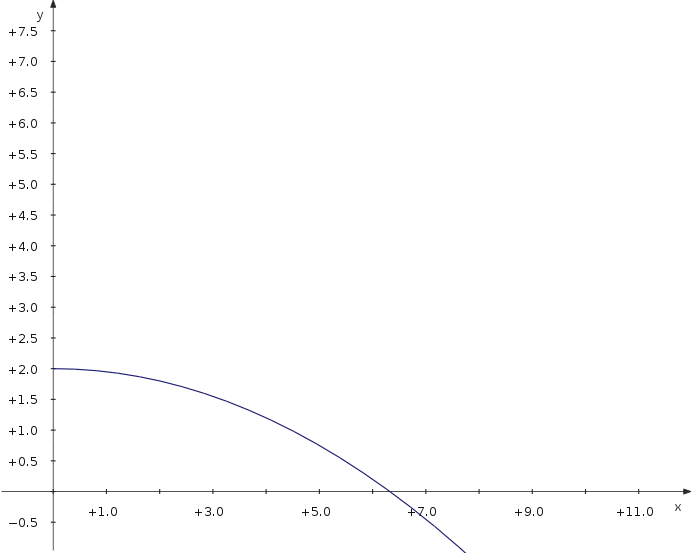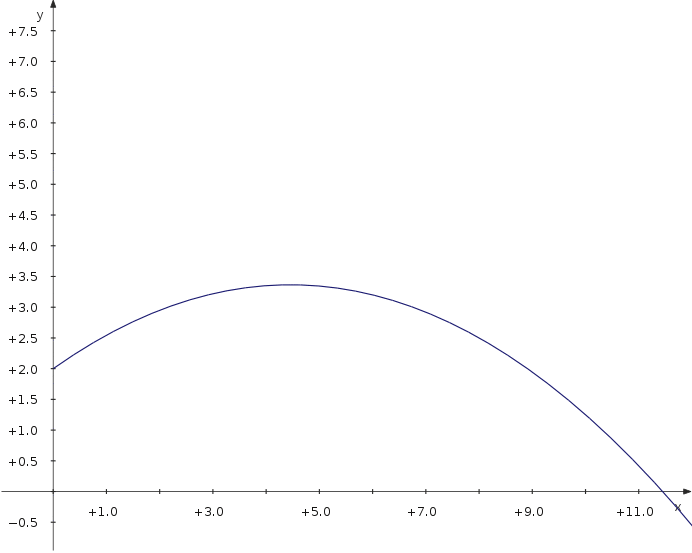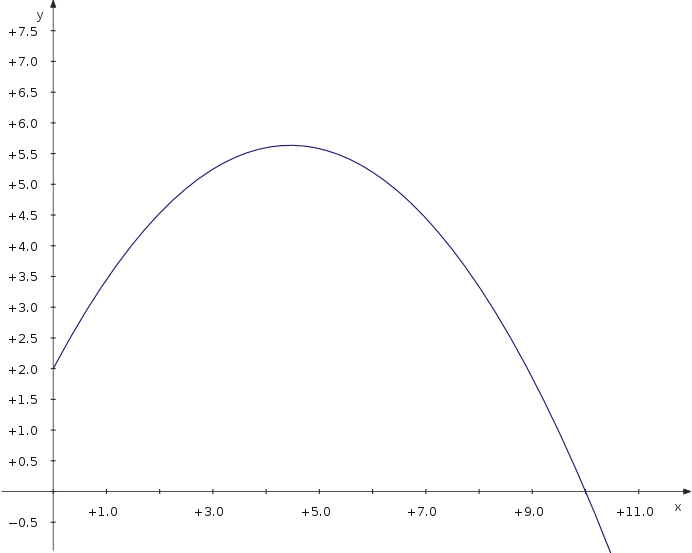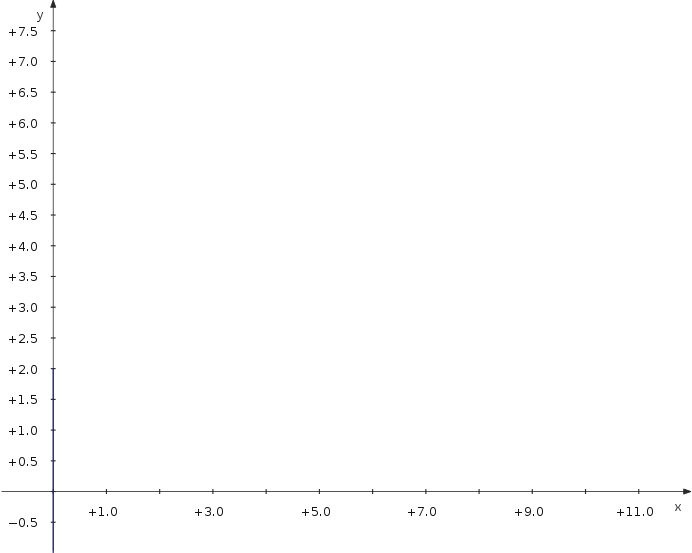
Вивчимо тепер питання щодо максимальної віддалі польоту снаряда в залежності від кута, під яким його було випущено. Для цього ми скористаємося параметричною кривою, параметром у якій буде кут. | |||
* | * Визначимо сталу v_0, що відповідає початковій швидкості. | ||
* | * Створимо нову параметричну функцію. | ||
* | * Введемо рівняння {{Input|1=<nowiki>f_x(t,α) = v_0∙cos(α)∙t | ||
f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2</nowiki>}} | f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2</nowiki>}} | ||
* | * Позначимо пункт <menuchoice>Повзунок</menuchoice> і виберемо <menuchoice>Повзунок 1</menuchoice> зі спадного списку. | ||
* | * Щоб зробити видимою панель повзунків, позначимо пункт <menuchoice>Перегляд -> Показати повзунки</menuchoice> | ||
Тепер можна пересувати повзунок і спостерігати за віддаллю, на яку відлетить снаряд в залежності від значення кута. | |||
[[Image:Kmplot_projectile.gif|center|692px|]] | [[Image:Kmplot_projectile.gif|center|692px|]] | ||
[[Category: | [[Category:Освіта/uk]] | ||
Latest revision as of 18:35, 11 October 2010
Однією з основних можливостей KmPlot є можливість візуалізації впливу параметрів на графік функції.
Пересування графіка синуса
Давайте навчимося пересувати графік синуса ліворуч і праворуч:
- Створіть новий графік у прямокутній декартовій системі координат.
- Введіть рівняння кривої
f(x,a) = sin(x-a)
- Позначте пункт і виберіть зі спадного списку.
- Щоб зробити повзунки видимими, позначте пункт
Тепер ви можете пересувати повзунок і спостерігати за тим, як значення параметра впливає на розташування кривої.
- Знімки вікон
-
Введення даних
-
Позначаємо пункт показу повзунків
-
Вікно повзунків
Траєкторія руху снаряда
Вивчимо тепер питання щодо максимальної віддалі польоту снаряда в залежності від кута, під яким його було випущено. Для цього ми скористаємося параметричною кривою, параметром у якій буде кут.
- Визначимо сталу v_0, що відповідає початковій швидкості.
- Створимо нову параметричну функцію.
- Введемо рівняння
f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2
- Позначимо пункт і виберемо зі спадного списку.
- Щоб зробити видимою панель повзунків, позначимо пункт
Тепер можна пересувати повзунок і спостерігати за віддаллю, на яку відлетить снаряд в залежності від значення кута.