KmPlot/Using Sliders/fr: Difference between revisions
Appearance
Created page with "Maintenant vous pouvez modifier la glissière et voir comment la valeur du paramètre modifie la position de la courbe." |
Created page with "<gallery perrow="3" caption="Captures d'écran"> Image:Kmplot_function_with_param.png|Entrée Image:Kmplot_view_show_sliders.png|Afficher les options de la glissière Image:Kmplo..." |
||
| Line 13: | Line 13: | ||
Maintenant vous pouvez modifier la glissière et voir comment la valeur du paramètre modifie la position de la courbe. | Maintenant vous pouvez modifier la glissière et voir comment la valeur du paramètre modifie la position de la courbe. | ||
<gallery perrow="3" caption=" | <gallery perrow="3" caption="Captures d'écran"> | ||
Image:Kmplot_function_with_param.png| | Image:Kmplot_function_with_param.png|Entrée | ||
Image:Kmplot_view_show_sliders.png| | Image:Kmplot_view_show_sliders.png|Afficher les options de la glissière | ||
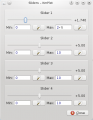
Image:Kmplot_sliders.png| | Image:Kmplot_sliders.png|Fenêtre de la glissière | ||
</gallery> | </gallery> | ||
Revision as of 21:32, 7 July 2012
Une fonctionnalité principale de KmPlot est de visualiser l'influence des paramètres d'une fonction sur une courbe.
Bouger une courbe de sinus
Regardons comment déplacer une courbe de sinus de gauche à droite :
- Créer une nouvelle courbe cartésienne
- Saisir l'équation
f(x,a) = sin(x-a)
- Vérifier l'option et choisir dans la liste déroulante.
- Pour rendre la glissière visible, vérifier
Maintenant vous pouvez modifier la glissière et voir comment la valeur du paramètre modifie la position de la courbe.
- Captures d'écran
-
Entrée
-
Afficher les options de la glissière
-
Fenêtre de la glissière
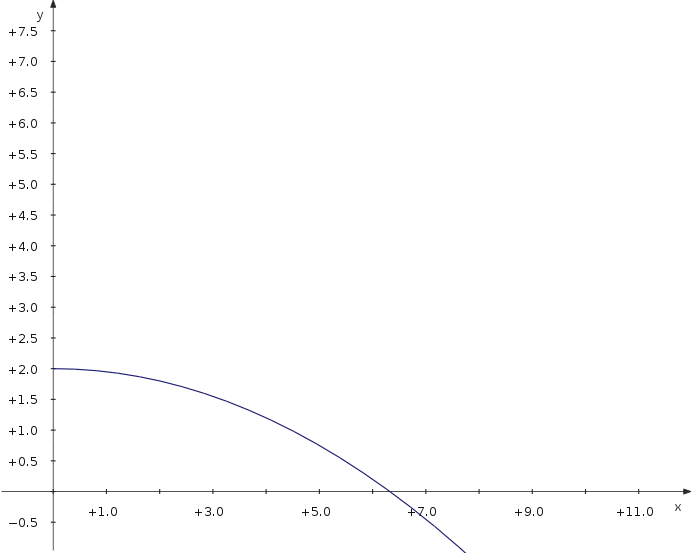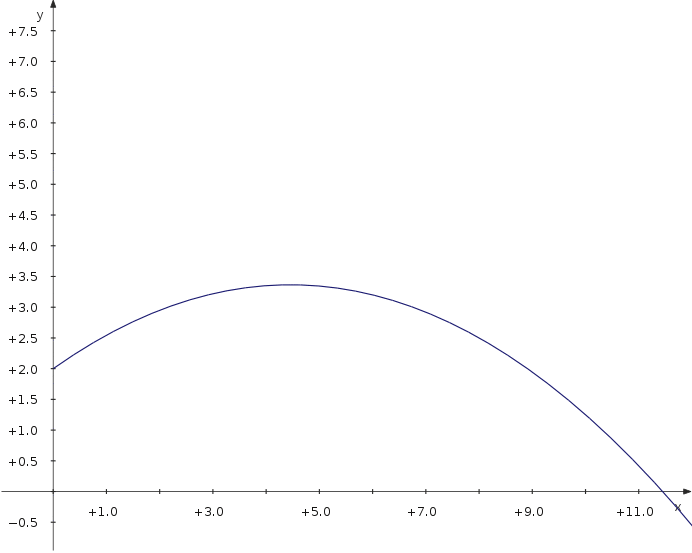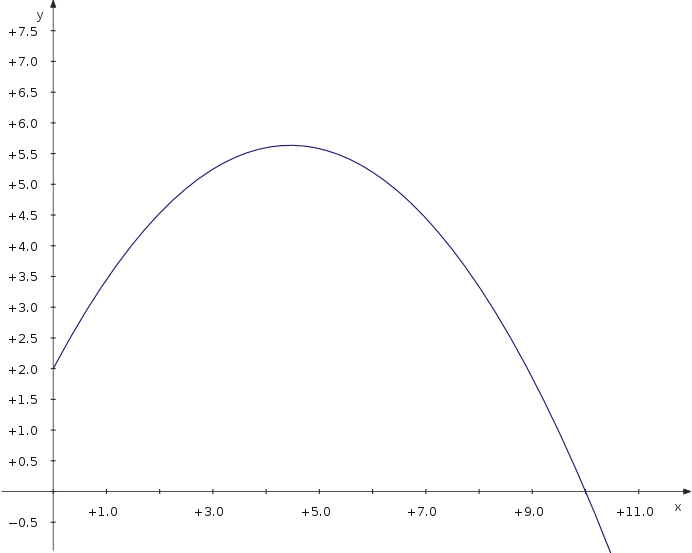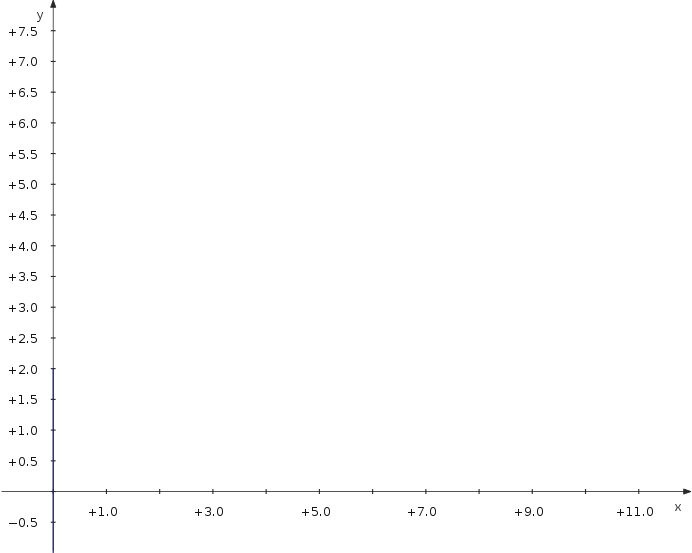
Trajectory of a Projectile
Now let's have a look at the maximum distance of a projectile thrown with different angles. We use a parametric plot depending on an additional parameter which is the angle.
- Define a constant v_0 for the starting velocity.
- Create a new parametric plot
- Enter the equations
f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2
- Check the option and choose from the drop down list.
- To make the available sliders visible, check
Now you can move the slider and see how the distance depends on the parameter value.