KmPlot/Using Sliders: Difference between revisions
Appearance
Pipesmoker (talk | contribs) Tutorial for sliders use |
Pipesmoker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
A main feature fo '''KmPlot''' is to visualize the influence of parameters to the curve of a function. Let's see, how to move a sinus curve left and right: | <languages /> | ||
<translate> | |||
A main feature fo '''KmPlot''' is to visualize the influence of parameters to the curve of a function. | |||
==Moving a Sinus Curve== | |||
Let's see, how to move a sinus curve left and right: | |||
* Create a new cartesian plot. | * Create a new cartesian plot. | ||
| Line 8: | Line 14: | ||
Now you can move the slider and see how the parameter value modifies the position of the curve. | Now you can move the slider and see how the parameter value modifies the position of the curve. | ||
==Screenshots== | ===Screenshots=== | ||
<gallery perrow="3"> | <gallery perrow="3"> | ||
| Line 15: | Line 21: | ||
Image:Kmplot_sliders.png|Slider window | Image:Kmplot_sliders.png|Slider window | ||
</gallery> | </gallery> | ||
==Trajectory of a Projectile== | |||
[[Image:Kmplot_projectile.png|thumb]] | |||
Now let's have a look at the maximum distance of a projectile thrown with different angles. We use a parametric plot depending on an additional parameter which is the angel. | |||
* Define a contant v_0 for the starting velocity. | |||
* Create a new parametric plot | |||
* Enter the equations {{Input|1=<nowiki>f_x(t,α) = v_0∙cos(α)∙t | |||
f_y(t,α) =2+ v_0∙sin(α)∙t−5∙t^2</nowiki>}} | |||
* Check the <menuchoice>Slider</menuchoice> option and choose <menuchoice>Slider No. 1</menuchoice> from the drop down list. | |||
* To make the available sliders visible, check <menuchoice>View -> Show Sliders</menuchoice> | |||
Now you can move the slider and see how the distance depends on the parameter value. | |||
{{Category:Education}} | |||
</translate> | |||
Revision as of 13:41, 11 October 2010
A main feature fo KmPlot is to visualize the influence of parameters to the curve of a function.
Moving a Sinus Curve
Let's see, how to move a sinus curve left and right:
- Create a new cartesian plot.
- Enter the equation
f(x,a) = sin(x-a)
- Check the option and choose from the drop down list.
- To make the available sliders visible, check
Now you can move the slider and see how the parameter value modifies the position of the curve.
Screenshots
-
Input
-
Show sliders option
-
Slider window
Trajectory of a Projectile
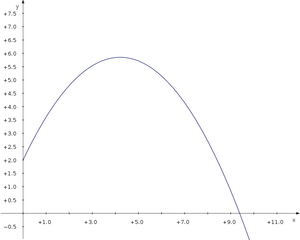
Now let's have a look at the maximum distance of a projectile thrown with different angles. We use a parametric plot depending on an additional parameter which is the angel.
- Define a contant v_0 for the starting velocity.
- Create a new parametric plot
- Enter the equations
f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) =2+ v_0∙sin(α)∙t−5∙t^2
- Check the option and choose from the drop down list.
- To make the available sliders visible, check
Now you can move the slider and see how the distance depends on the parameter value. Educational and training fun for young and old