KAlgebra/Домашня робота
На цій сторінці наведено приклади застосування KAlgebra для розв’язання конкретних задач.
Приклад з комбінаторики
Нехай слід визначити кількість способів, якими можна розсадити 6 осіб (p1, p2 ... p6) навколо круглого столу з 6 стільцями.
Очевидно, можливі такі варіанти:
p1 p2 p3 p4 p5 p6 p1 p2 p3 p4 p6 p5 p1 p2 p3 p5 p4 p6 p1 p2 p3 p5 p6 p4
і так далі.
Можна зауважити, що останню позицію за столом можна заповнити лише у один спосіб, передостанню — у 2, далі — у 3, у 4, у 5, і нарешті у 6 способів. Отже загальну кількість варіантів можна визначити за допомогою простої формули:
6*5*4*3*2*1
Введемо цю формулу у консоль KAlgebra, і програма обчислить відповідь:
(((((1)*2)*3)*4)*5)*6 =720
Подібний розподіл значень за варіантами, де кількість значень дорівнює кількості варіантів називається «переставляннями».
Ви можете скористатися функцією KAlgebra для обчислення кількості таких переставлянь (ця функція називається «факторіал»):
factorial(6)
дасть нам
factorial(6) =720
Як бачите, ми отримали той самий результат.
Приклад з теорії ймовірностей
Визначимо ймовірність викинути певну грань гральної кістки.
Сприятливим для нас буде викидання відповідної грані, а несприятливим - викидання інших граней.
Отже, сприятливим буде лише один варіант із шести:
- ймовірність = кількість вибраних граней / загальна кількість граней = 1/6
Отже тепер ми знаємо, що ймовірність викидання певної грані кістки дорівнює 1/6.
Ви можете створити просту функцію у KAlgebra для отримання значення ймовірності за означенням:
jmovirnist:=(spryyatlyvi,zagalom)->spryyatlyvi/zagalom
Теорія чисел
Нехай нам потрібно визначити суму всіх цілих чисел у певному діапазоні, наприклад, від 1 до 100. Знаходження подібної суми без певної вправності у арифметиці (якщо ви знаєте потрібний прийом, це нескладно) справа доволі марудна.
У KAlgebra передбачено чудові можливості для виконання подібних обчислень. Віддайте у консолі такі команди:
sum(x: x=1..100)
в результаті отримаємо:
sum(x: x=1..100) = 5050
Вказана нами синтаксична конструкція призначена для виконання такої послідовності дій:
- 1. Обмежити діапазон значень x
- 2. Взяти перше значення x
- 3. Взяти друге значення x і додати попереднє значення x
- 4. Взяти третє значення x і додати попереднє значення x
- ...
- N. Взяти останнє значення x і додати останнє значення x
Розрахунок електричних ланцюгів
Приклад 1
Розглянемо простий елемент множення з двома вхідними портами та одним вихідним. Для визначення результату у KAlgebra можна скористатися таким кодом:
and(var1, var2)
Ми отримаємо результат логічного множення вхідних змінних.
Приклад 2
Розглянемо простий електричний ланцюг: джерело живлення з напругою 3 В та два елементи опору (R1 і R2) з’єднані паралельно з опором 3 кОм. Потрібно визначити струм, який проходитиме ланцюгом.
Для початку визначимо значення загального опору відповідно до такого закону:
- Rзаг = (1/R1 + 1/R2)-1
- I = U/Rзаг
Давайте створимо просту функцію у KAlgebra для виконання обчислень за вказаними формулами:
R_zag:=(R1,R2)->(1/R1+1/R2)^-1
I:=(U,R_zag)->U/R_zag
Подивимося, що у нас вийшло:
I(3, R_zag(3000, 3000))
I(3, R_zag(3 000, 3 000)) = 0,002
Теплопровідність
Приклад з однаковими матеріалами, але різними об’ємами та температурами
Now, what if we need to know the final temperature when we mix 40L of 15°C water with 30L of 70°C water?
Using conservation of energy, we know that the initial and final thermal energies are the same, so the final energy is equal to the energy of the first fluid plus the energy of the second fluid(using U for internal energy):
- U(final) = U1 + U2
Internal energy is equal to the volumetric heat capacity times volume times temperature:
- U = C*V*T
So C(final)*V(final)*T(final) = C1*V1*T1 + C2*V2*T2
And since the heat capacities are all the same and cancel out, and the final volume is the sum of the two initial volumes:
- (V1+V2)*T(final) = V1*T1 + V2*T2
- or
- T(final) = (V1*T1 + V2*T2)/(V1+V2)
We can then either use this directly in KAlgebra:
(40*15 + 30*70)/(40 + 30)
(40*15+30*70)/(40+30) =38.5714
and get the final temperature, or put in a function if we need to repeat the computation:
finalTemp:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)
Which we can then use like this:
finalTemp(40,15,30,70)
finalTemp(40, 15, 30, 70) =38.5714
Example Problem with Different Fluids
Now, suppose the two fluids have different volumetric heat capacities, such as 4180 J/(L*K) for the first liquid (water), and 1925 J/(L*K) for the second liquid (ethanol).
We will need to refer back to the equation:
- C(final)*V(final)*T(final) = C1*V1*T1 + C2*V2*T2
The resultant heat capacity will be the average of the capacities of the first and second fluids, weighted by volume(since it is a volumetric heat capacity rather than mass- or molar-specific):
- C(final) = (C1*V1 + C2*V2)/V(final)
And plugging this into the previous equation, we get:
- (C1*V1 + C2*V2)*T(final) = C1*V1*T1 + C2*V2*T2
- or
- T(final) = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)
And either use this formula directly:
(4180*40*15 + 1925*30*70)/(4180*40+1925*30)
((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30) =29.1198
Or write a function if we want to repeat the calculation:
finalTemp2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2)
Which we can then use like this:
finalTemp2(4180,40,15,1925,30,70)
finalTemp2(4,180, 40, 15, 1,925, 30, 70) =29.1198
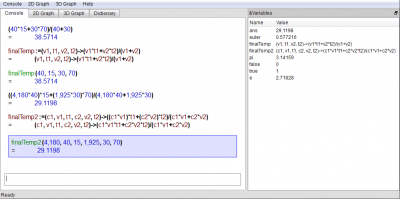
Screenshot of KAlgebra after running these computations: