KAlgebra/Homework
This page shows some uses of KAlgebra in real world problems.
Combinatorial example
We have 6 people who want to know how to get around a table with 6 chairs.
We know that 6 people can get around the table with this configuration
p1 p2 p3 p4 p5 p6 p1 p2 p3 p4 p6 p5 p1 p2 p3 p5 p4 p6 p1 p2 p3 p5 p6 p4
And so on.
We notice that the last item rotates its position by 1, the fifth rotates position by 2, the fourth rotates position by 3, the third rotates position by 4, the second rotates position by 5 and first rotates position by 6. So we can write down a simple formula:
6*5*4*3*2*1
Let's write this into KAlgebra console, and the answer returned is:
(((((1)*2)*3)*4)*5)*6 =720
This kind of arrangement of things around some position, where the position number is equal to the number of things, is called "permutation".
Let's try to call in KAlgebra the permutation function:
factorial(6)
and we get
factorial(6) =720
It's the same result as you can see.
Probability example
Let's roll a dice. We want to know the probability of one face appearing.
We can define positive probability, the result of the event being favourable to us, and negative probability, the result of the event being unfavourable to us.
So you have to pick only one face:
- probability = face picked / total face = 1/6
So now we know that when a dice is rolled there is a 1/6 of probability that a face we chose will come up.
We can set a simple function in KAlgebra to take this formula in a simple way:
probability:=(favorable,total)->favorable/total
Numerical Theory
Let's say that we want to know the sum of all numbers between a bounded interval, for instance 1 - 100. We have to do the sum of all numbers from 0 to 100 if we don't know the rule to get them.
KAlgebra offers a great facility to this task. Let's write in console:
sum(x: x=1..100)
and we get the result:
sum(x: x=1..100) = 5050
The syntax indicate this:
- 1. Bound x as variable
- 2. Take first value of x
- 3. Take second value of x and add the previous value of x
- 4. Take third value of x and add the previous value of x
- ...
- N. Take the last value of x and add the last value of x
Electronic
Example 1
Let's take a simple AND gate with two inputs and one output. To resolve it in KAlgebra we will write
and(variable1, variable2)
from which we will get the and value of the input as output.
Example 2
We have a simple circuit: a battery of 3V and two electrical resistances (R1 and R2) put on parallel of 3kOhm. We want to get the current circulating in the circuit.
We have first to calculate the value of the electric resistance expressed according to the law:
- TotalResistance = (1/R1 + 1/R2)-1
- Current = Voltage/TotalResistance
Let's write a simple function in KAlgebra to do this:
totalresistance:=(R1,R2)->(1/R1+1/R2)^-1
current:=(voltage,totalresistance)->voltage/totalresistance
Let's see what we get:
current(3, totalresistance(3000, 3000))
current(3, totalresistance(3 000, 3 000)) = 0,002
Fluid
Example Problem with Same Material, but Different Volumes and Temperatures
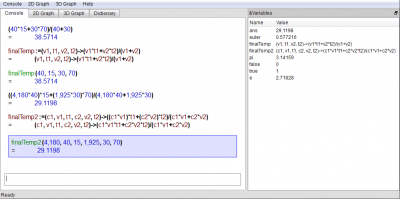
Now, what if we need to know the final temperature when we mix 40L of 15°C water with 30L of 70°C water?
Using conservation of energy, we know that the initial and final thermal energies are the same, so the final energy is equal to the energy of the first fluid plus the energy of the second fluid(using U for internal energy):
- Ufinal = U1 + U2
Internal energy is equal to the volumetric heat capacity times volume times temperature:
- U = C*V*T
So Cfinal*Vfinal*Tfinal = C1*V1*T1 + C2*V2*T2
And since the heat capacities are all the same and cancel out, and the final volume is the sum of the two initial volumes:
- (V1+V2)*Tfinal = V1*T1 + V2*T2
- or
- Tfinal = (V1*T1 + V2*T2)/(V1+V2)
We can then either use this directly in KAlgebra:
(40*15 + 30*70)/(40 + 30)
(40*15+30*70)/(40+30) =38.5714
and get the final temperature, or put in a function if we need to repeat the computation:
finalTemp:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)
Which we can then use like this:
finalTemp(40,15,30,70)
finalTemp(40, 15, 30, 70) =38.5714
Example Problem with Different Fluids
Now, suppose the two fluids have different volumetric heat capacities, such as 4180 J/(L*K) for the first liquid (water), and 1925 J/(L*K) for the second liquid (ethanol).
We will need to refer back to the equation:
- Cfinal*Vfinal*Tfinal = C1*V1*T1 + C2*V2*T2
The resultant heat capacity will be the average of the capacities of the first and second fluids, weighted by volume(since it is a volumetric heat capacity rather than mass- or molar-specific):
- Cfinal = (C1*V1 + C2*V2)/Vfinal
And plugging this into the previous equation, we get:
- (C1*V1 + C2*V2)*Tfinal = C1*V1*T1 + C2*V2*T2
- or
- Tfinal = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)
And either use this formula directly:
(4180*40*15 + 1925*30*70)/(4180*40+1925*30)
((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30) =29.1198
Or write a function if we want to repeat the calculation:
finalTemp2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2)
Which we can then use like this:
finalTemp2(4180,40,15,1925,30,70)
finalTemp2(4,180, 40, 15, 1,925, 30, 70) =29.1198
Screenshot of KAlgebra after running these computations: