KAlgebra/Homework/it: Difference between revisions
Importing a new version from external source |
No edit summary |
||
| (19 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<languages /> | <languages /> | ||
Questa pagina mostra alcuni utilizzi di '''KAlgebra''' in problemi reali. | Questa pagina mostra alcuni utilizzi di '''KAlgebra''' in problemi reali. | ||
== Esempio di calcolo combinatorio == | == Esempio di calcolo combinatorio == | ||
| Line 79: | Line 79: | ||
===Esempio 1=== | ===Esempio 1=== | ||
Prendiamo una semplice porta AND con due ingressi e un'uscita. Per risolverlo in '''KAlgebra''' scriveremo: | |||
Prendiamo | |||
{{Input|1=and(variabile1, variabile2)}} | {{Input|1=and(variabile1, variabile2)}} | ||
da cui otterremo come risultato il valore and di ingresso. | |||
da cui otterremo come risultato il valore di ingresso. | |||
===Esempio 2=== | ===Esempio 2=== | ||
| Line 95: | Line 91: | ||
Dobbiamo prima calcolare il valore della resistenza elettrica espressa secondo la legge: | Dobbiamo prima calcolare il valore della resistenza elettrica espressa secondo la legge: | ||
:ResistenzaTotale = (1/R1 + 1/R2) | :ResistenzaTotale = (1/R1 + 1/R2)<sup>-1</sup> | ||
:Attuale = Voltaggio/ResistenzaTotale | :Attuale = Voltaggio/ResistenzaTotale | ||
| Line 113: | Line 109: | ||
===Esempio di problema con stesso materiale, ma differenti volumi e temperature=== | ===Esempio di problema con stesso materiale, ma differenti volumi e temperature=== | ||
Ora che facciamo se abbiamo bisogno di sapere la temperatura finale quando mescoliamo 40L di acqua a 15°C con 30L di acqua a 70°C? | Ora che facciamo se abbiamo bisogno di sapere la temperatura finale quando mescoliamo 40L di acqua a 15°C con 30L di acqua a 70°C? | ||
Tenendo conto della conservazione dell'energia sappiamo che le energie termiche iniziali e finali sono le stesse, dunque l'energia finale è uguale all'energia del primo fluido più l'energia del secondo (utilizzando U per l'energia interna):<br> | Tenendo conto della conservazione dell'energia sappiamo che le energie termiche iniziali e finali sono le stesse, dunque l'energia finale è uguale all'energia del primo fluido più l'energia del secondo (utilizzando U per l'energia interna):<br /> | ||
:U | :U<sub>finale</sub> = U1 + U2 | ||
L'energia interna è uguale alla capacità termica del volume per il volume e per la temperatura:<br /> | |||
L'energia interna è uguale alla capacità termica del volume per il volume e per la temperatura:<br> | |||
:U = C*V*T | :U = C*V*T | ||
Dunque C | Dunque C<sub>finale</sub>*V<sub>finale</sub>*T<sub>finale</sub> = C1*V1*T1 + C2*V2*T2 | ||
E dato che le capacità termiche sono tutte le stesse e si annullano e che il volume finale è la somma dei due volumi iniziali:<br /> | |||
E dato che le capacità termiche sono tutte le stesse e si annullano e che il volume finale è la somma dei due volumi iniziali:<br> | :(V1+V2)*T<sub>finale</sub> = V1*T1 + V2*T2 | ||
:(V1+V2)*T | |||
::o | ::o | ||
:T | :T<sub>finale</sub> = (V1*T1 + V2*T2)/(V1+V2) | ||
Possiamo quindi utilizzare questa direttamente in KAlgebra: | Possiamo quindi utilizzare questa direttamente in '''KAlgebra''': | ||
{{Input |<nowiki>(40*15 + 30*70)/(40 + 30) | {{Input |<nowiki>(40*15 + 30*70)/(40 + 30) | ||
</nowiki>}} | </nowiki>}} | ||
| Line 151: | Line 141: | ||
Ora supponiamo che due fluidi abbiano differenti capacità termiche per volume come 4180 J/(L*K) per il primo liquido(acqua) e 1925 J/(L*K) per il secondo (etanolo). | Ora supponiamo che due fluidi abbiano differenti capacità termiche per volume come 4180 J/(L*K) per il primo liquido(acqua) e 1925 J/(L*K) per il secondo (etanolo). | ||
Avremo bisogno di riprendere l'equazione:<br /> | Avremo bisogno di riprendere l'equazione:<br /> | ||
:C | :C<sub>finale</sub>*V<sub>finale</sub>*T<sub>finale</sub> = C1*V1*T1 + C2*V2*T2 | ||
La capacità termica risultante sarà la media delle capacità del primo e del secondo fluido, ponderata per il volume(dato che si tratta di capacità termica per volume piuttosto che di quella specifica per la massa o per le moli):<br /> | La capacità termica risultante sarà la media delle capacità del primo e del secondo fluido, ponderata per il volume(dato che si tratta di capacità termica per volume piuttosto che di quella specifica per la massa o per le moli):<br /> | ||
:C | :C<sub>finale</sub> = (C1*V1 + C2*V2)/V<sub>finale</sub> | ||
E collegando questo nell'equazione precedente otteniamo:<br /> | E collegando questo nell'equazione precedente otteniamo:<br /> | ||
:(C1*V1 + C2*V2)*T | :(C1*V1 + C2*V2)*T<sub>finale</sub> = C1*V1*T1 + C2*V2*T2 | ||
::o | ::o | ||
:T | :T<sub>finale</sub> = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2) | ||
E utilizzando questa formula direttamente: | E utilizzando questa formula direttamente: | ||
| Line 179: | Line 169: | ||
[[Image:KAlgebra-Fluids-Example-Screenshot.png|400px|center]] | [[Image:KAlgebra-Fluids-Example-Screenshot.png|400px|center]] | ||
[[Category: | [[Category:Istruzione/it]] | ||
Latest revision as of 14:15, 30 July 2011
Questa pagina mostra alcuni utilizzi di KAlgebra in problemi reali.
Esempio di calcolo combinatorio
Abbiamo 6 persone che vogliono sapere come mettersi attorno a un tavolo con 6 sedie.
Sappiamo che le 6 persone possono posizionarsi attorno al tavolo in questa configurazione:
p1 p2 p3 p4 p5 p6 p1 p2 p3 p4 p6 p5 p1 p2 p3 p5 p4 p6 p1 p2 p3 p5 p6 p4
E così via.
Notiamo che l'ultimo elemento si sposta di 1, il quinto di 2, il quarto di 3, il terzo di 4, il secondo di 5 e il primo di 6. Possiamo quindi scrivere una semplice formula:
6*5*4*3*2*1
Scriviamola nella console di KAlgebra e la risposta in uscita sarà:
(((((1)*2)*3)*4)*5)*6 =720
Questo modo di organizzare le cose spostandole di alcune posizioni, in cui il numero della posizione è uguale al numero delle cose stesse, è chiamato "permutazione".
Proviamo a calcolare in KAlgebra la funzione di permutazione:
factorial(6)
e otteniamo
factorial(6) =720
Come puoi vedere è lo stesso risultato.
Esempio di calcolo della probabilità
Lanciamo un dado. Vogliamo sapere la probabilità di ottenere un certo numero.
Possiamo definire probabilità positiva il risultato dell'evento a noi favorevole e probabilità negativa il risultato sfavorevole.
Devi quindi scegliere una sola faccia del dado:
- probabilità = faccia scelta / facce totali = 1/6
Ora quindi sappiamo che quando lanciamo un dado c'è 1/6 di probabilità di ottenere la faccia che abbiamo scelto.
Possiamo impostare una semplice funzione in KAlgebra per prendere questa formula in modo facile:
probabilità:=(favorevole,totale)->favorevole/totale
Teoria dei numeri
Diciamo che vogliamo sapere la somma di tutti i numeri compresi in un dato intervallo, per esempio 1 - 100. Dobbiamo sommare tutti i numeri da 0 a 100 se non conosciamo la regola.
KAlgebra offre un'ottima semplificazione per questa operazione. Scriviamo nella console:
sum(x: x=1..100)
e otteniamo il risultato:
sum(x: x=1..100) = 5050
La sintassi indica questo:
- 1. Limite x come variabile
- 2. Prendere il primo valore di x
- 3. Prendere il secondo valore di x e aggiungere il precedente
- 4. Prendere il terzo valore di x e aggiungere il precedente
- ...
- N. Prendere l'ultimo valore di x e aggiungere l'ultimo.
Elettronica
Esempio 1
Prendiamo una semplice porta AND con due ingressi e un'uscita. Per risolverlo in KAlgebra scriveremo:
and(variabile1, variabile2)
da cui otterremo come risultato il valore and di ingresso.
Esempio 2
Abbiamo un semplice circuito: una batteria da 3V e due resistenze da 3kOhm (R1 e R2) messe in parallelo. Vogliamo conoscere la corrente che passa nel circuito.
Dobbiamo prima calcolare il valore della resistenza elettrica espressa secondo la legge:
- ResistenzaTotale = (1/R1 + 1/R2)-1
- Attuale = Voltaggio/ResistenzaTotale
Scriviamo una semplice funzione in KAlgebra per farlo:
resistenzatotale:=(R1,R2)->(1/R1+1/R2)^-1
attuale:=(voltaggio,resistenzatotale)->voltaggio/resistenzatotale
Vediamo che otteniamo:
attuale(3, resistenzatotale(3000, 3000))
attuale(3, resistenzatotale(3 000, 3 000)) = 0,002
Fluidi
Esempio di problema con stesso materiale, ma differenti volumi e temperature
Ora che facciamo se abbiamo bisogno di sapere la temperatura finale quando mescoliamo 40L di acqua a 15°C con 30L di acqua a 70°C?
Tenendo conto della conservazione dell'energia sappiamo che le energie termiche iniziali e finali sono le stesse, dunque l'energia finale è uguale all'energia del primo fluido più l'energia del secondo (utilizzando U per l'energia interna):
- Ufinale = U1 + U2
L'energia interna è uguale alla capacità termica del volume per il volume e per la temperatura:
- U = C*V*T
Dunque Cfinale*Vfinale*Tfinale = C1*V1*T1 + C2*V2*T2
E dato che le capacità termiche sono tutte le stesse e si annullano e che il volume finale è la somma dei due volumi iniziali:
- (V1+V2)*Tfinale = V1*T1 + V2*T2
- o
- Tfinale = (V1*T1 + V2*T2)/(V1+V2)
Possiamo quindi utilizzare questa direttamente in KAlgebra:
(40*15 + 30*70)/(40 + 30)
(40*15+30*70)/(40+30) =38.5714
ed ottenere la temperatura finale o metterla in una funzione se abbiamo bisogno di ripetere il calcolo:
TemperaturaFinale:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)
Che possiamo poi utilizzare così:
TemperaturaFinale(40,15,30,70)
TemperaturaFinale(40, 15, 30, 70) =38.5714
Esempio di problema con diversi fluidi
Ora supponiamo che due fluidi abbiano differenti capacità termiche per volume come 4180 J/(L*K) per il primo liquido(acqua) e 1925 J/(L*K) per il secondo (etanolo).
Avremo bisogno di riprendere l'equazione:
- Cfinale*Vfinale*Tfinale = C1*V1*T1 + C2*V2*T2
La capacità termica risultante sarà la media delle capacità del primo e del secondo fluido, ponderata per il volume(dato che si tratta di capacità termica per volume piuttosto che di quella specifica per la massa o per le moli):
- Cfinale = (C1*V1 + C2*V2)/Vfinale
E collegando questo nell'equazione precedente otteniamo:
- (C1*V1 + C2*V2)*Tfinale = C1*V1*T1 + C2*V2*T2
- o
- Tfinale = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)
E utilizzando questa formula direttamente:
(4180*40*15 + 1925*30*70)/(4180*40+1925*30)
((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30) =29.1198
Oppure scriviamo una funzione se vogliamo ripetere il calcolo:
TemperaturaFinale2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 +c2*v2*t2)/(c1*v1+c2*v2)
Che possiamo poi utilizzare così:
TemperaturaFinale2(4180,40,15,1925,30,70)
TemperaturaFinale2(4,180, 40, 15, 1,925, 30, 70) =29.1198
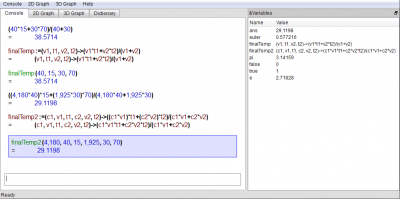
Schermata di KAlgebra dopo aver eseguito questi calcoli: