KAlgebra/Homework/da: Difference between revisions
Importing a new version from external source |
Importing a new version from external source |
||
| (57 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Denne side viser, hvordan '''KAlgebra''' kan bruges til at løse opgaver fra den virkelige verden. | Denne side viser, hvordan '''KAlgebra''' kan bruges til at løse opgaver fra den virkelige verden. | ||
== | == Eksempel med kombinatorik == | ||
Vi har 6 personer, som vil vide, på hvor mange måder de kan fordele sig omkring et bord med 6 stole. | |||
Vi ved, at 6 personer kan fordele sig omkring bordet med disse konfigurationer | |||
:{| | :{| | ||
| Line 18: | Line 18: | ||
|} | |} | ||
og så videre. | |||
Vi bemærker, at den første person kan placere sig på 6 forskellige pladser; den anden person har så 5 muligheder for at placere sig, og herefter er der 4 pladser til den tredje person, så 3 pladser til fjerde, 2 pladser til den femte og endelig 1 plads til den sjette. Vi kan således skrive følgende simple beregning: | |||
{{Input | 1=6*5*4*3*2*1}} | {{Input | 1=6*5*4*3*2*1}} | ||
Det skriver vi i '''KAlgebras''' konsol, og får svaret: | |||
{{Output | 1=<nowiki>(((((1)*2)*3)*4)*5)*6 | {{Output | 1=<nowiki>(((((1)*2)*3)*4)*5)*6 | ||
=720</nowiki>}} | =720</nowiki>}} | ||
Den slags arrangementer af ting i rækkefølger, hvor antallet af pladser er lig med antallet af ting kaldes en permutation. | |||
Lad os prøve at bruge '''KAlgebras''' permutationsfunktion: | |||
{{Input|1=factorial(6)}} | {{Input|1=factorial(6)}} så får vi | ||
{{Output|1=<nowiki>factorial(6) | {{Output|1=<nowiki>factorial(6) | ||
=720</nowiki>}} | =720</nowiki>}} | ||
Som du kan se, giver det samme resultat som før. | |||
== | == Eksempel med sandsynligheder == | ||
Lad os kaste med en terning. Vi vil finde sandsynligheden for et bestemt udfald. | |||
Vi taler om positivt udfald, når kastet falder ud til vores fordel og negativt udfald, når det ikke er fordelagtigt for os. | |||
: | Her skal du altså vælge en bestemt side: | ||
:Sandsynlighed = antal sider valgt/samlet antal sider = 1/6 | |||
Nu ved vi, at når terningen kastes, så er der 1/6 chance for, at terningen lander med vores side opad. | |||
Vi kan definere en simpel funktion i '''KAlgebra''' til at beregne dette: | |||
== | {{Input|1=<nowiki>sandsynlighed:=(favorabel,total)->favorabel/total</nowiki>}} | ||
== Talteori == | |||
'''KAlgebra''' | Lad os sige, at vi ønsker at kende summen af alle tal i et begrænset interval, for eksempel fra 1 til 100. Vi skal så lægge alle disse hundrede tal sammen, hvis vi ikke kender en formel, der kan bruges. | ||
'''KAlgebra''' har en smart funktion til denne opgave. Vi skriver i konsollen: | |||
{{Input|1= sum(x: x=1..100)}} | {{Input|1= sum(x: x=1..100)}} | ||
og får resultatet: | |||
{{Output|1=<nowiki>sum(x: x=1..100) | {{Output|1=<nowiki>sum(x: x=1..100) | ||
= 5050</nowiki>}} | = 5050</nowiki>}} | ||
Der sker følgende: | |||
:1. | :1. Brug x som variabel | ||
:2. | :2. Tag den første værdi af x | ||
:3. | :3. Tag den anden værdi af x og læg det til den første værdi | ||
:4. | :4. Tag den tredje værdi af x og læg den til den forrige sum | ||
::... | ::... | ||
:N. | :N. Tag den sidste værdi af x og læg den til den forrige sum | ||
== Elektronik == | |||
== | === Eksempel 1 === | ||
Lad os tage en simpel AND-kreds med to input og et output. For at simulere det i '''KAlgebra''' skriver vi | |||
{{Input|1=and(variabel1, variabel2)}} | |||
hvilket vil beregne det output, som kredsen giver med de to input. | |||
=== Eksempel 2 === | |||
Vi har et simpelt kredsløb bestående af et 3V-batteri og to elektriske modstande (R1 og R2) på hver 3 kOhm forbundet parallelt. Vi vil beregne strømmen i kredsløbet. | |||
Først skal vi beregne værdien af den elektriske modstand ved hjælp af følgende formel: | |||
: | :SamletModstand = (1/R1 + 1/R2)<sup>-1</sup> | ||
: | :Strøm = Spænding/SamletModstand | ||
LAd os skrive a enkel funktion i '''KAlgebra''' til at gøre dette: | |||
{{Input|1= | {{Input|1=samletmodstand:=(R1,R2)->(1/R1+1/R2)^-1 | ||
strøm:=(spænding,samletmodstand)->spænding/samletmodstand}} | |||
Lad os se, hvad vi får: | |||
{{Input|1= | {{Input|1=strøm(3, samletmodstand(3000, 3000))}} | ||
{{Output|1=<nowiki> | {{Output|1=<nowiki>strøm(3, samletmodstand(3 000, 3 000)) | ||
= 0,002</nowiki>}} | = 0,002</nowiki>}} | ||
== | == Væsker == | ||
=== | === Eksempel med samme væsker men forskellige rumfang og temperaturer === | ||
Hvad nu, hvis vi vil vide, hvad sluttemperaturen bliver, når vi blander 40 L 15°C varmt vand med 30 L 70°C varmt vand? Ved at bruge energibevarelse ved vi, at den samlede termiske energi er den samme før og efter blandingen, så slutenergien er lig med summen af energierne i de to væsker (vi bruger U for intern energi):<br /> | |||
:U<sub>final</sub> = U1 + U2 | :U<sub>final</sub> = U1 + U2 | ||
Intern energi er lig med den volumetriske varmecapacitet ganget med temperaturen:<br /> | |||
:U = C*V*T | :U = C*V*T | ||
Så C<sub>slut</sub>*V<sub>slut</sub>*T<sub>slut</sub> = C1*V1*T1 + C2*V2*T2 | |||
Da varmekapaciteterne alle er ens, så går de ud, og slutvolumenet er lig summen af de to oprindelige volumener:<br /> | |||
:(V1+V2)*T<sub> | :(V1+V2)*T<sub>slut</sub> = V1*T1 + V2*T2 | ||
:: | ::eller | ||
:T<sub> | :T<sub>slut</sub> = (V1*T1 + V2*T2)/(V1+V2) | ||
Vi kan enten udregne dette direkte i '''KAlgebra''':{{Input |<nowiki>(40*15 + 30*70)/(40 + 30) | |||
{{Input |<nowiki>(40*15 + 30*70)/(40 + 30) | |||
</nowiki>}} | </nowiki>}} | ||
{{Output |<nowiki>(40*15+30*70)/(40+30) | {{Output |<nowiki>(40*15+30*70)/(40+30) | ||
=38.5714</nowiki>}} | =38.5714</nowiki>}} | ||
for at finde sluttemperaturen eller vi kan definere en funktion, hvis vi skal gentage beregningen: | |||
{{Input |<nowiki> | {{Input |<nowiki>slutTemp:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)</nowiki>}} | ||
Den kan vi så bruge således: | |||
{{Input |<nowiki>finalTemp(40,15,30,70) | {{Input |<nowiki>finalTemp(40,15,30,70) | ||
</nowiki>}} | </nowiki>}} | ||
| Line 137: | Line 135: | ||
=38.5714</nowiki>}} | =38.5714</nowiki>}} | ||
=== | === Eksempel med forskellige væsker === | ||
Antag nu, at de to væsker har forskellige volumetriske varmekapaciteter; for eksempel 4180 J/(L*K) for den første (vand) og 1925 J/(L*K) for den anden (sprit). Vi skal igen bruge formlen:<br /> | |||
:C<sub>slut</sub>*V<sub>slut</sub>*T<sub>slut</sub> = C1*V1*T1 + C2*V2*T2 | |||
:C<sub> | |||
Varmekapaciteten af blandingen vil være gennemsnittet af de to oprindelige varmekapaciteter vægtet efter volumen (eftersom det er volumetriske varmekapaciteter):<br /> | |||
:C<sub> | :C<sub>slut</sub> = (C1*V1 + C2*V2)/V<sub>slut</sub> | ||
Indsætter vi i de foregående ligninger får vi:<br /> | |||
:(C1*V1 + C2*V2)*T<sub> | :(C1*V1 + C2*V2)*T<sub>slut</sub> = C1*V1*T1 + C2*V2*T2 | ||
:: | ::eller | ||
:T<sub> | :T<sub>slut</sub> = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2) | ||
Vi kan enten bruge denne formel direkte: | |||
{{Input |<nowiki>(4180*40*15 + 1925*30*70)/(4180*40+1925*30) | {{Input |<nowiki>(4180*40*15 + 1925*30*70)/(4180*40+1925*30) | ||
</nowiki>}} | </nowiki>}} | ||
| Line 157: | Line 154: | ||
=29.1198</nowiki>}} | =29.1198</nowiki>}} | ||
Eller skrive en funktion, hvis vi skal gentage beregningen: | |||
{{Input |<nowiki> | {{Input |<nowiki>slutTemp2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2) | ||
</nowiki>}} | </nowiki>}} | ||
Den kan vi så bruge således: | |||
{{Input |<nowiki> | {{Input |<nowiki>slutTemp2(4180,40,15,1925,30,70) | ||
</nowiki>}} | </nowiki>}} | ||
{{Output |<nowiki> | {{Output |<nowiki>slutTemp2(4,180, 40, 15, 1,925, 30, 70) | ||
=29.1198</nowiki>}} | =29.1198</nowiki>}} | ||
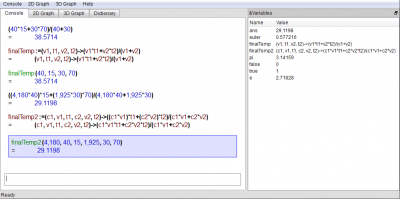
Skærmbillede af '''KAlgebra''' efter at have lavet disse beregninger: | |||
[[Image:KAlgebra-Fluids-Example-Screenshot.png|400px|center]] | [[Image:KAlgebra-Fluids-Example-Screenshot.png|400px|center]] | ||
[[Category: | [[Category:Uddannelse/da]] | ||
Latest revision as of 17:21, 29 April 2011
Denne side viser, hvordan KAlgebra kan bruges til at løse opgaver fra den virkelige verden.
Eksempel med kombinatorik
Vi har 6 personer, som vil vide, på hvor mange måder de kan fordele sig omkring et bord med 6 stole.
Vi ved, at 6 personer kan fordele sig omkring bordet med disse konfigurationer
p1 p2 p3 p4 p5 p6 p1 p2 p3 p4 p6 p5 p1 p2 p3 p5 p4 p6 p1 p2 p3 p5 p6 p4
og så videre.
Vi bemærker, at den første person kan placere sig på 6 forskellige pladser; den anden person har så 5 muligheder for at placere sig, og herefter er der 4 pladser til den tredje person, så 3 pladser til fjerde, 2 pladser til den femte og endelig 1 plads til den sjette. Vi kan således skrive følgende simple beregning:
6*5*4*3*2*1
Det skriver vi i KAlgebras konsol, og får svaret:
(((((1)*2)*3)*4)*5)*6 =720
Den slags arrangementer af ting i rækkefølger, hvor antallet af pladser er lig med antallet af ting kaldes en permutation.
Lad os prøve at bruge KAlgebras permutationsfunktion:
factorial(6)
så får vi
factorial(6) =720
Som du kan se, giver det samme resultat som før.
Eksempel med sandsynligheder
Lad os kaste med en terning. Vi vil finde sandsynligheden for et bestemt udfald.
Vi taler om positivt udfald, når kastet falder ud til vores fordel og negativt udfald, når det ikke er fordelagtigt for os.
Her skal du altså vælge en bestemt side:
- Sandsynlighed = antal sider valgt/samlet antal sider = 1/6
Nu ved vi, at når terningen kastes, så er der 1/6 chance for, at terningen lander med vores side opad.
Vi kan definere en simpel funktion i KAlgebra til at beregne dette:
sandsynlighed:=(favorabel,total)->favorabel/total
Talteori
Lad os sige, at vi ønsker at kende summen af alle tal i et begrænset interval, for eksempel fra 1 til 100. Vi skal så lægge alle disse hundrede tal sammen, hvis vi ikke kender en formel, der kan bruges.
KAlgebra har en smart funktion til denne opgave. Vi skriver i konsollen:
sum(x: x=1..100)
og får resultatet:
sum(x: x=1..100) = 5050
Der sker følgende:
- 1. Brug x som variabel
- 2. Tag den første værdi af x
- 3. Tag den anden værdi af x og læg det til den første værdi
- 4. Tag den tredje værdi af x og læg den til den forrige sum
- ...
- N. Tag den sidste værdi af x og læg den til den forrige sum
Elektronik
Eksempel 1
Lad os tage en simpel AND-kreds med to input og et output. For at simulere det i KAlgebra skriver vi
and(variabel1, variabel2)
hvilket vil beregne det output, som kredsen giver med de to input.
Eksempel 2
Vi har et simpelt kredsløb bestående af et 3V-batteri og to elektriske modstande (R1 og R2) på hver 3 kOhm forbundet parallelt. Vi vil beregne strømmen i kredsløbet.
Først skal vi beregne værdien af den elektriske modstand ved hjælp af følgende formel:
- SamletModstand = (1/R1 + 1/R2)-1
- Strøm = Spænding/SamletModstand
LAd os skrive a enkel funktion i KAlgebra til at gøre dette:
samletmodstand:=(R1,R2)->(1/R1+1/R2)^-1
strøm:=(spænding,samletmodstand)->spænding/samletmodstand
Lad os se, hvad vi får:
strøm(3, samletmodstand(3000, 3000))
strøm(3, samletmodstand(3 000, 3 000)) = 0,002
Væsker
Eksempel med samme væsker men forskellige rumfang og temperaturer
Hvad nu, hvis vi vil vide, hvad sluttemperaturen bliver, når vi blander 40 L 15°C varmt vand med 30 L 70°C varmt vand? Ved at bruge energibevarelse ved vi, at den samlede termiske energi er den samme før og efter blandingen, så slutenergien er lig med summen af energierne i de to væsker (vi bruger U for intern energi):
- Ufinal = U1 + U2
Intern energi er lig med den volumetriske varmecapacitet ganget med temperaturen:
- U = C*V*T
Så Cslut*Vslut*Tslut = C1*V1*T1 + C2*V2*T2
Da varmekapaciteterne alle er ens, så går de ud, og slutvolumenet er lig summen af de to oprindelige volumener:
- (V1+V2)*Tslut = V1*T1 + V2*T2
- eller
- Tslut = (V1*T1 + V2*T2)/(V1+V2)
Vi kan enten udregne dette direkte i KAlgebra:
(40*15 + 30*70)/(40 + 30)
(40*15+30*70)/(40+30) =38.5714
for at finde sluttemperaturen eller vi kan definere en funktion, hvis vi skal gentage beregningen:
slutTemp:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)
Den kan vi så bruge således:
finalTemp(40,15,30,70)
finalTemp(40, 15, 30, 70) =38.5714
Eksempel med forskellige væsker
Antag nu, at de to væsker har forskellige volumetriske varmekapaciteter; for eksempel 4180 J/(L*K) for den første (vand) og 1925 J/(L*K) for den anden (sprit). Vi skal igen bruge formlen:
- Cslut*Vslut*Tslut = C1*V1*T1 + C2*V2*T2
Varmekapaciteten af blandingen vil være gennemsnittet af de to oprindelige varmekapaciteter vægtet efter volumen (eftersom det er volumetriske varmekapaciteter):
- Cslut = (C1*V1 + C2*V2)/Vslut
Indsætter vi i de foregående ligninger får vi:
- (C1*V1 + C2*V2)*Tslut = C1*V1*T1 + C2*V2*T2
- eller
- Tslut = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)
Vi kan enten bruge denne formel direkte:
(4180*40*15 + 1925*30*70)/(4180*40+1925*30)
((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30) =29.1198
Eller skrive en funktion, hvis vi skal gentage beregningen:
slutTemp2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2)
Den kan vi så bruge således:
slutTemp2(4180,40,15,1925,30,70)
slutTemp2(4,180, 40, 15, 1,925, 30, 70) =29.1198
Skærmbillede af KAlgebra efter at have lavet disse beregninger: