KmPlot/Using Sliders/fr: Difference between revisions
Appearance
Created page with "* Définir une constante v_0 pour la vitesse initiale. * Créer une courbe paramétrique * Saisir les équations {{Input|1=<nowiki>f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) = 2+v_0..." |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Une fonctionnalité principale de '''KmPlot''' est de visualiser l'influence des paramètres d'une fonction sur une courbe. | Une fonctionnalité principale de '''KmPlot''' est de visualiser l'influence des paramètres d'une fonction sur une courbe. | ||
== | == Déplacer une courbe de sinus == | ||
Regardons comment déplacer une courbe de sinus de gauche à droite : | Regardons comment déplacer une courbe de sinus de gauche à droite : | ||
| Line 30: | Line 30: | ||
* Pour rendre les glissières visibles, vérifier <menuchoice>Affichage -> Afficher les glissières</menuchoice> | * Pour rendre les glissières visibles, vérifier <menuchoice>Affichage -> Afficher les glissières</menuchoice> | ||
Maintenant vous pouvez modifier la glissière et voir comment la distance évolue avec la valeur du paramètre. | |||
[[Image:Kmplot_projectile.gif|center|692px|]] | [[Image:Kmplot_projectile.gif|center|692px|]] | ||
[[Category: | [[Category:Éducation/fr ]] | ||
Latest revision as of 21:41, 7 July 2012
Une fonctionnalité principale de KmPlot est de visualiser l'influence des paramètres d'une fonction sur une courbe.
Déplacer une courbe de sinus
Regardons comment déplacer une courbe de sinus de gauche à droite :
- Créer une nouvelle courbe cartésienne
- Saisir l'équation
f(x,a) = sin(x-a)
- Vérifier l'option et choisir dans la liste déroulante.
- Pour rendre la glissière visible, vérifier
Maintenant vous pouvez modifier la glissière et voir comment la valeur du paramètre modifie la position de la courbe.
- Captures d'écran
-
Entrée
-
Afficher les options de la glissière
-
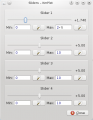
Fenêtre de la glissière
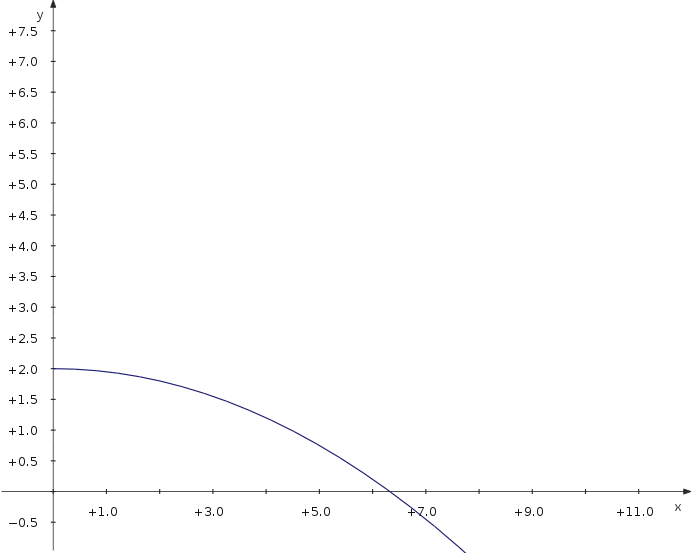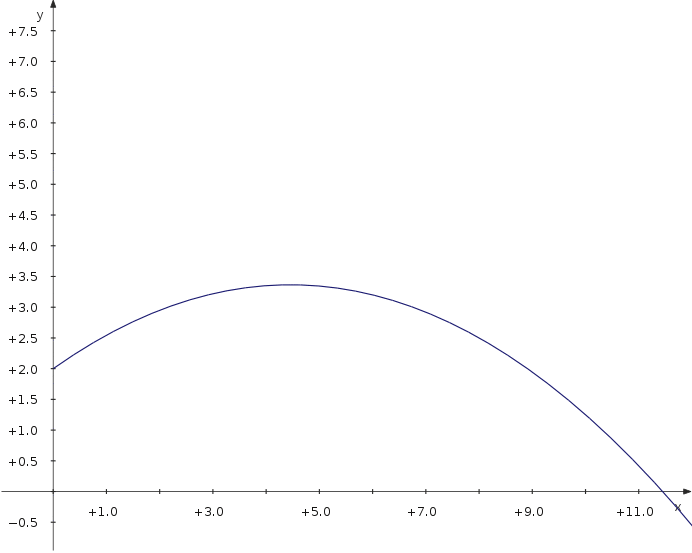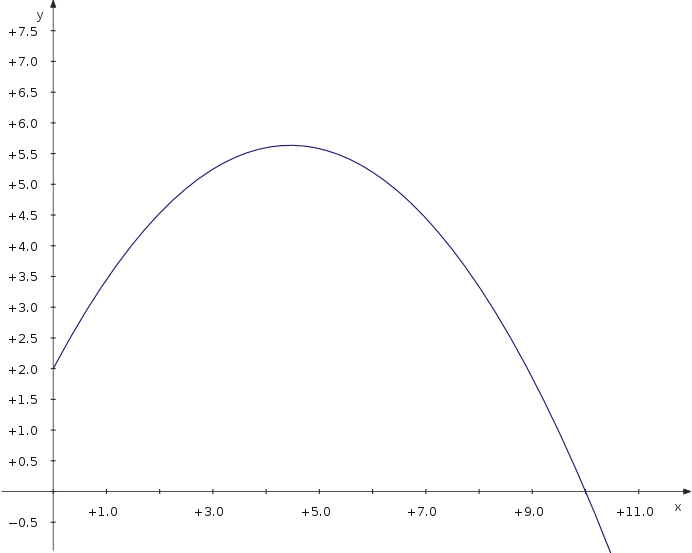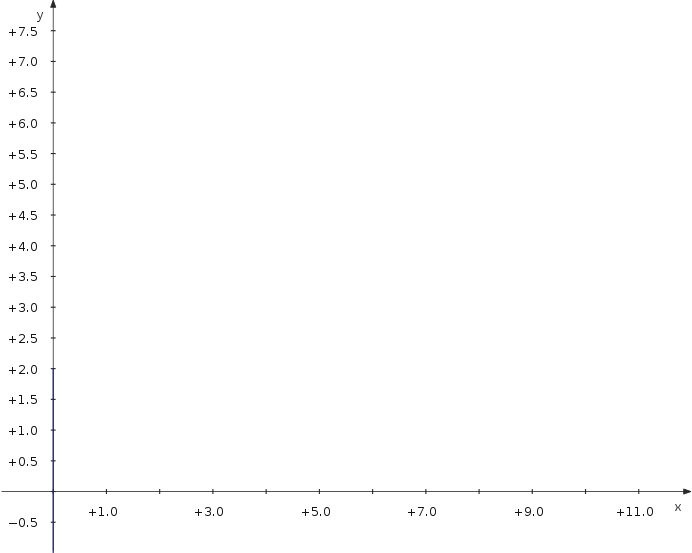
Trajectoire d'un projectile
Maintenant intéressons nous à la distance maximale d'un projectile lancé avec différents angles. Nous utilisons une courbe paramétrique qui dépend d'un paramètre additionnel qui est l'angle.
- Définir une constante v_0 pour la vitesse initiale.
- Créer une courbe paramétrique
- Saisir les équations
f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2
- Vérifier l'option et choisir dans le menu déroulant.
- Pour rendre les glissières visibles, vérifier
Maintenant vous pouvez modifier la glissière et voir comment la distance évolue avec la valeur du paramètre.