KAlgebra/Homework/it

Questa pagina mostra alcuni utilizzi di KAlgebra in problemi reali. \

Esempio di calcolo combinatorio

Abbiamo 6 persone che vogliono sapere come mettersi attorno a un tavolo con 6 sedie.

Sappiamo che le 6 persone possono posizionarsi attorno al tavolo in questa configurazione:

p1	p2	p3	p4	p5	p6
p1	p2	p3	p4	p6	p5
p1	p2	p3	p5	p4	p6
p1	p2	p3	p5	p6	p4

E così via.

Notiamo che l'ultimo elemento si sposta di 1, il quinto di 2, il quarto di 3, il terzo di 4, il secondo di 5 e il primo di 6. Possiamo quindi scrivere una semplice formula:

6*5*4*3*2*1

Scriviamola nella console di KAlgebra e la risposta in uscita sarà:

(((((1)*2)*3)*4)*5)*6
=720

Questo modo di organizzare le cose spostandole di alcune posizioni, in cui il numero della posizione è uguale al numero delle cose stesse, è chiamato "permutazione".

Proviamo a calcolare in KAlgebra la funzione di permutazione:

factorial(6)

e otteniamo

factorial(6)
=720

Come puoi vedere è lo stesso risultato.

Esempio di calcolo della probabilità

Lanciamo un dado. Vogliamo sapere la probabilità di ottenere un certo numero.

Possiamo definire probabilità positiva il risultato dell'evento a noi favorevole e probabilità negativa il risultato sfavorevole.

Devi quindi scegliere una sola faccia del dado:

probabilità = faccia scelta / facce totali = 1/6

So now we know that when a dice is rolled there is a 1/6 of probability that a face we chose will come up.

We can set a simple function in KAlgebra to take this formula in a simple way:

probability:=(favorable,total)->favorable/total

Numerical Theory

Let's say that we want to know the sum of all numbers between a bounded interval, for instance 1 - 100. We have to do the sum of all numbers from 0 to 100 if we don't know the rule to get them.

KAlgebra offers a great facility to this task. Let's write in console:

sum(x: x=1..100)

and we get the result:

sum(x: x=1..100)
= 5050

The syntax indicate this:

1. Bound x as variable

2. Take first value of x

3. Take second value of x and add the previous value of x

4. Take third value of x and add the previous value of x

...

N. Take the last value of x and add the last value of x

Electronic

Example 1

Let's take a simple circuit a and port with two inputs and one output. To resolve it in KAlgebra we will write

and(variable1, variable2)

from which we will get the and value of the input as output.

Example 2

We have a simple circuit: a battery of 3V and two electrical resistances (R1 and R2) put on parallel of 3kOhm. We want to get the current circulating in the circuit.

We have first to calculate the value of the electric resistance expressed according to the law:

TotalResistance = (1/R1 + 1/R2)^-1

Current = Voltage/TotalResistance

Let's write a simple function in KAlgebra to do this:

totalresistance:=(R1,R2)->(1/R1+1/R2)^-1
current:=(voltage,totalresistance)->voltage/totalresistance

Let's see what we get:

current(3, totalresistance(3000, 3000))

current(3, totalresistance(3 000, 3 000))
= 0,002

Fluid

Example Problem with Same Material, but Different Volumes and Temperatures

Now, what if we need to know the final temperature when we mix 40L of 15°C water with 30L of 70°C water? Using conservation of energy, we know that the initial and final thermal energies are the same, so the final energy is equal to the energy of the first fluid plus the energy of the second fluid(using U for internal energy):

U(final) = U1 + U2

Internal energy is equal to the volumetric heat capacity times volume times temperature:

U = C*V*T

So C(final)*V(final)*T(final) = C1*V1*T1 + C2*V2*T2

And since the heat capacities are all the same and cancel out, and the final volume is the sum of the two initial volumes:

(V1+V2)*T(final) = V1*T1 + V2*T2

or

T(final) = (V1*T1 + V2*T2)/(V1+V2)

We can then either use this directly in KAlgebra:

(40*15 + 30*70)/(40 + 30)

(40*15+30*70)/(40+30)
=38.5714

and get the final temperature, or put in a function if we need to repeat the computation:

finalTemp:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)

Which we can then use like this:

finalTemp(40,15,30,70)

finalTemp(40, 15, 30, 70)
=38.5714

Example Problem with Different Fluids

Now, suppose the two fluids have different volumetric heat capacities, such as 4180 J/(L*K) for the first liquid (water), and 1925 J/(L*K) for the second liquid (ethanol). We will need to refer back to the equation:

C(final)*V(final)*T(final) = C1*V1*T1 + C2*V2*T2

The resultant heat capacity will be the average of the capacities of the first and second fluids, weighted by volume(since it is a volumetric heat capacity rather than mass- or molar-specific):

C(final) = (C1*V1 + C2*V2)/V(final)

And plugging this into the previous equation, we get:

(C1*V1 + C2*V2)*T(final) = C1*V1*T1 + C2*V2*T2

or

T(final) = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)

And either use this formula directly:

(4180*40*15 + 1925*30*70)/(4180*40+1925*30)

((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30)
=29.1198

Or write a function if we want to repeat the calculation:

finalTemp2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2)

Which we can then use like this:

finalTemp2(4180,40,15,1925,30,70)

finalTemp2(4,180, 40, 15, 1,925, 30, 70)
=29.1198

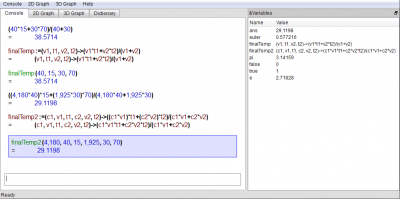
Screenshot of KAlgebra after running these computations: