KAlgebra/Homework/da

Denne side viser, hvordan KAlgebra kan bruges til at løse opgaver fra den virkelige verden.

Eksempel med kombinatorik

Vi har 6 personer, som vil vide, på hvor mange måder de kan fordele sig omkring et bord med 6 stole.

Vi ved, at 6 personer kan fordele sig omkring bordet med disse konfigurationer

p1	p2	p3	p4	p5	p6
p1	p2	p3	p4	p6	p5
p1	p2	p3	p5	p4	p6
p1	p2	p3	p5	p6	p4

og så videre.

Vi bemærker, at den første person kan placere sig på 6 forskellige pladser; den anden person har så 5 muligheder for at placere sig, og herefter 4 pladser til den tredje person, så 3 pladser til fjerde, 2 pladser til den femte og endelig 1 plads til den sjette. Vi kan således skrive følgende simple beregning:

6*5*4*3*2*1

Det skriver vi i KAlgebras konsol, og får svaret:

(((((1)*2)*3)*4)*5)*6
=720

Den slags arrangementer af ting i rækkefølger, hvor antallet af pladser er lig med antallet af ting kaldes en permutation.

Lad os prøve at bruge KAlgebras permutationsfunktion:

factorial(6)

så får vi

factorial(6)
=720

Som du kan se, giver det samme resultat som før.

Eksempel med sandsynligheder

Lad os kaste med en terning. Vi vil finde sandsynligheden for et bestemt udfald.

Vi taler om positivt udfald, når kastet falder ud til vores fordel og negativt udfald, når det ikke er fordelagtigt for os.

Her skal du altså vælge en bestemt side:

Sandsynlighed = antal sider valgt/samlet antal sider = 1/6

Nu ved vi, at når terningen kastes, så er der 1/6 chance for, at terningen lander med vores side opad.

Vi kan definere en simpel funktion i KAlgebra til at beregne dette:

probability:=(favorable,total)->favorable/total

Numerical Theory

Let's say that we want to know the sum of all numbers between a bounded interval, for instance 1 - 100. We have to do the sum of all numbers from 0 to 100 if we don't know the rule to get them.

KAlgebra offers a great facility to this task. Let's write in console:

sum(x: x=1..100)

and we get the result:

sum(x: x=1..100)
= 5050

The syntax indicate this:

1. Bound x as variable

2. Take first value of x

3. Take second value of x and add the previous value of x

4. Take third value of x and add the previous value of x

...

N. Take the last value of x and add the last value of x

Electronic

Example 1

Let's take a simple AND gate with two inputs and one output. To resolve it in KAlgebra we will write

and(variable1, variable2)

from which we will get the and value of the input as output.

Example 2

We have a simple circuit: a battery of 3V and two electrical resistances (R1 and R2) put on parallel of 3kOhm. We want to get the current circulating in the circuit.

We have first to calculate the value of the electric resistance expressed according to the law:

TotalResistance = (1/R1 + 1/R2)^-1

Current = Voltage/TotalResistance

Let's write a simple function in KAlgebra to do this:

totalresistance:=(R1,R2)->(1/R1+1/R2)^-1
current:=(voltage,totalresistance)->voltage/totalresistance

Let's see what we get:

current(3, totalresistance(3000, 3000))

current(3, totalresistance(3 000, 3 000))
= 0,002

Fluid

Example Problem with Same Material, but Different Volumes and Temperatures

Now, what if we need to know the final temperature when we mix 40L of 15°C water with 30L of 70°C water? Using conservation of energy, we know that the initial and final thermal energies are the same, so the final energy is equal to the energy of the first fluid plus the energy of the second fluid(using U for internal energy):

U_final = U1 + U2

Internal energy is equal to the volumetric heat capacity times volume times temperature:

U = C*V*T

So C_final*V_final*T_final = C1*V1*T1 + C2*V2*T2

And since the heat capacities are all the same and cancel out, and the final volume is the sum of the two initial volumes:

(V1+V2)*T_final = V1*T1 + V2*T2

or

T_final = (V1*T1 + V2*T2)/(V1+V2)

We can then either use this directly in KAlgebra:

(40*15 + 30*70)/(40 + 30)

(40*15+30*70)/(40+30)
=38.5714

and get the final temperature, or put in a function if we need to repeat the computation:

finalTemp:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)

Which we can then use like this:

finalTemp(40,15,30,70)

finalTemp(40, 15, 30, 70)
=38.5714

Example Problem with Different Fluids

Now, suppose the two fluids have different volumetric heat capacities, such as 4180 J/(L*K) for the first liquid (water), and 1925 J/(L*K) for the second liquid (ethanol). We will need to refer back to the equation:

C_final*V_final*T_final = C1*V1*T1 + C2*V2*T2

The resultant heat capacity will be the average of the capacities of the first and second fluids, weighted by volume(since it is a volumetric heat capacity rather than mass- or molar-specific):

C_final = (C1*V1 + C2*V2)/V_final

And plugging this into the previous equation, we get:

(C1*V1 + C2*V2)*T_final = C1*V1*T1 + C2*V2*T2

or

T_final = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)

And either use this formula directly:

(4180*40*15 + 1925*30*70)/(4180*40+1925*30)

((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30)
=29.1198

Or write a function if we want to repeat the calculation:

finalTemp2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2)

Which we can then use like this:

finalTemp2(4180,40,15,1925,30,70)

finalTemp2(4,180, 40, 15, 1,925, 30, 70)
=29.1198

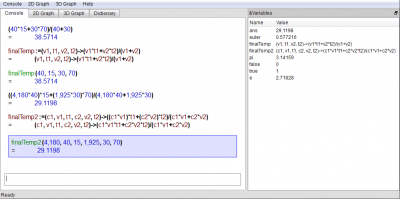
Screenshot of KAlgebra after running these computations: